简单线性回归

提示

线性回归（Linear Regression）是一种常见的统计学和机器学习方法，用于建立自变量（特征）和因变量之间的线性关系模型。

本次所用到的数据集点击此处下载studentscores.csv

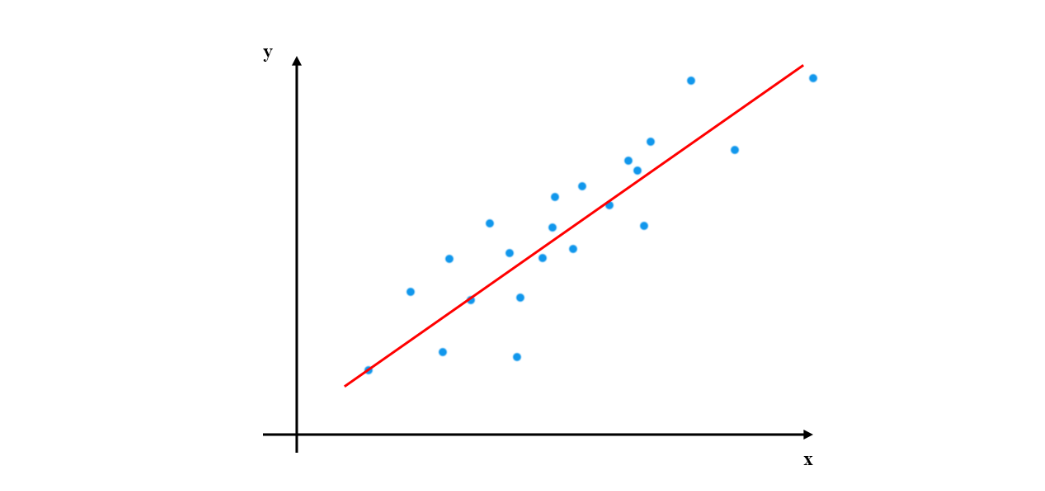
线性回归介绍

简单线性回归

在简单线性回归中，我们只有一个自变量和一个因变量。线性回归模型可以表示为：

$$y=wx+b$$

其中，$y$是因变量，$x$是自变量，$w$是自变量的权重（系数），$b$是偏置（截距）。我们的目标是通过最小化预测值与实际观测值之间的差异，找到最佳的$w$和$b$。

多元线性回归

多元线性回归涉及多个自变量和一个因变量。线性回归模型可以表示为：

$$y=w_1{x}_1+w_2{x}_2+\dots +w_n{x}_n+b$$

其中，$x_1,x_2,\dots ,x_n$是自变量（特征），$w_1,w_2,\dots ,w_n$是对应的权重（系数），$b$是偏置（截距）。

拟合直线

线性回归的目标是找到最佳拟合直线，使得预测值与实际观测值之间的差异最小化。最常用的方法是最小二乘法，通过最小化残差平方和来估计权重和偏置。

当使用最小二乘法进行线性回归时，假设我们有一个数据集，其中包含了学生的学习时间（自变量）和他们在考试中获得的分数（因变量）。我们想建立一个线性模型，来预测学生的考试分数。

假设我们的数据集如下：

学习时间（小时）	考试分数
2	65
3	70
4	80
5	85
6	90

我们可以使用最小二乘法来估计线性回归模型中的权重和偏置。

首先，计算自变量和因变量的平均值：

x_mean = (2 + 3 + 4 + 5 + 6) / 5 = 4
y_mean = (65 + 70 + 80 + 85 + 90) / 5 = 78

然后，计算权重 w：

w = Σ((xi - x_mean) * (yi - y_mean)) / Σ(xi - x_mean)^2
  = ((2-4)*(65-78) + (3-4)*(70-78) + (4-4)*(80-78) + (5-4)*(85-78) + (6-4)*(90-78)) / ((2-4)^2 + (3-4)^2 + (4-4)^2 + (5-4)^2 + (6-4)^2)
  = 5.8

最后，计算偏置 b：

b = y_mean - w * x_mean
  = 78 - 5.8 * 4
  = 55.2

因此，最小二乘法估计得到的线性回归模型为：

y = 5.8x + 55.2

这个模型可以用来预测学生在考试中的分数，基于他们的学习时间。例如，如果一个学生学习了7个小时，我们可以使用这个模型来估计他的考试分数：

y = 5.8 * 7 + 55.2
  = 97.4

根据最小二乘法估计的模型，预测该学生的考试分数约为97.4分。

1. 数据预处理

import pandas as pd

# 读取CSV文件
dataset = pd.read_csv('../data/studentscores.csv')

# 将自变量（特征）和因变量存储在X和Y中
X = dataset.iloc[:,:1].values
Y = dataset.iloc[:,-1].values

首先，我们使用pandas库读取了一个CSV文件，然后将自变量（特征）存储在变量X中，因变量存储在变量Y中。

训练集和测试集划分

from sklearn.model_selection import train_test_split

# 将数据集划分为训练集和测试集
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.2, random_state=0)

我们使用train_test_split函数将数据集划分为训练集和测试集。其中，test_size=0.2表示将20%的数据分配给测试集，random_state=0用于设置随机种子，以确保每次划分结果一致。

2.训练集使用简单线性回归模型来训练

from sklearn.linear_model import LinearRegression

# 创建并训练简单线性回归模型
regressor = LinearRegression()
regressor.fit(X_train, Y_train)

我们使用sklearn库的LinearRegression类创建了一个简单线性回归模型，并使用训练集数据对模型进行训练。

3.预测结果

# 使用训练好的模型对测试集进行预测
Y_pred = regressor.predict(X_test)

我们使用训练好的模型对测试集数据进行预测，并将结果存储在变量Y_pred中。

4.可视化

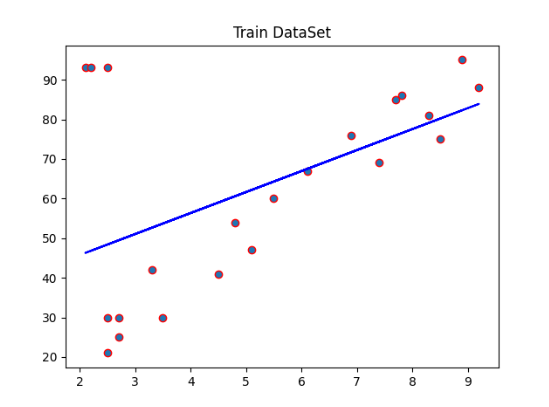
4.1 训练集结果可视化

import matplotlib.pyplot as plt

# 绘制训练集的实际观测值和预测值的散点图
plt.scatter(X_train, Y_train, edgecolors='red')

# 绘制训练集的拟合直线
plt.plot(X_train, regressor.predict(X_train), color='blue')

# 显示图形
plt.show()

我们使用matplotlib库绘制了训练集的实际观测值和预测值的散点图，并在图上绘制了训练集的拟合直线。

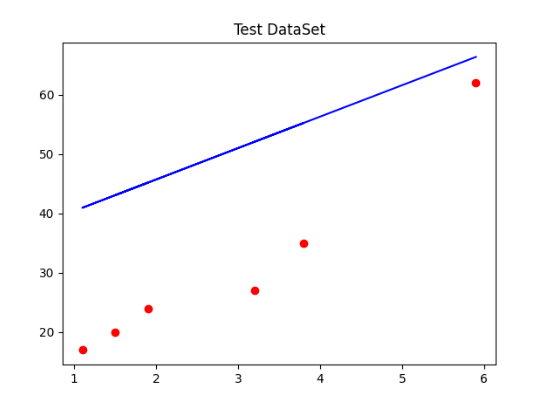
4.2 测试集可视化

import matplotlib.pyplot as plt

# 绘制测试集的实际观测值和预测值的散点图
plt.scatter(X_test, Y_test, color='red')

# 绘制测试集的拟合直线
plt.plot(X_test, regressor.predict(X_test), color='blue')

# 显示图形
plt.show()

最后，我们使用matplotlib库绘制了测试集的实际观测值和预测值的散点图，并在图上绘制了测试集的拟合直线。