逻辑回归(一)

当我们探索机器学习算法时，逻辑回归是一个不可忽视的重要工具。逻辑回归是一种广泛应用于分类问题的监督学习算法。它建立在线性回归的基础上，并通过一种称为“逻辑函数”的转换，将输出限制在0和1之间，从而实现对二分类问题的建模。本文将从线性回归出发，引导您深入了解逻辑回归的原理和应用。

首先，让我们回顾一下线性回归。在线性回归中，我们假设特征与目标之间存在线性关系，通过拟合一个最佳拟合直线来预测连续值的目标变量。然而，在分类问题中，我们的目标是将实例分类为两个不同的类别，例如判断一封电子邮件是否为垃圾邮件。这时，线性回归并不适用，因为它的输出范围是连续的。

1. 线性回归回顾

在线性回归中，我们假设特征与目标之间存在线性关系，通过拟合最佳拟合直线来预测连续值的目标变量。线性回归模型的表示形式为：

$$y=w_0+w_1{x}_1+w_2{x}_2+\dots +w_n{x}_n$$

其中，$y$ 是目标变量，$w_i$ 是特征 $x_i$ 的权重。

2. 引入逻辑函数

逻辑回归的思想是通过引入一个称为“逻辑函数”或“sigmoid函数”的非线性函数，将线性回归的输出转换为概率值。逻辑函数具有S形曲线，将任意实数映射到0和1之间。它的数学形式如下所示：

$$f(x)=\frac{1}{1+e^{-x}}$$

其中，$x$ 是线性回归的输出。通过这个转换，我们可以将线性回归的输出解释为相应类别的概率。当概率大于或等于一个阈值时，我们将实例分类为正类；当概率小于阈值时，我们将实例分类为负类。

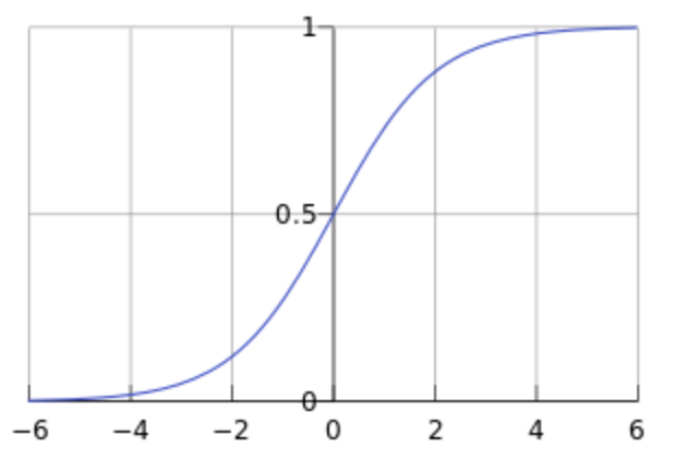
3. 逻辑回归模型的推导

为了推导逻辑回归模型，我们需要定义一个概率模型，该模型可以通过逻辑函数将线性回归的输出转换为概率值。假设我们的目标是预测二分类问题，其中类别标签为0和1。

首先，我们假设给定输入 $x$ 的条件下，目标变量 $y$ 的概率分布服从伯努利分布。伯努利分布是二项分布的特例，表示一个试验只有两个可能结果的情况。

我们定义 $P(y=1|x)$ 为给定输入 $x$ 下目标变量为1的概率，那么目标变量为0的概率可以表示为 $P(y=0|x)=1-P(y=1|x)$。

为了建立与线性回归的联系，我们使用对数几率（log odds）的概念，定义为：

$$\log \left(\frac{P(y=1|x)}{1-P(y=1|x)}\right)=w_0+w_1{x}_1+w_2{x}_2+\dots +w_n{x}_n$$

通过对上述方程进行变换和整理，我们可以得到逻辑回归模型的形式：

$$P(y=1|x)=\frac{1}{1+e^{-(w_0+w_1{x}_1+w_2{x}_2+\dots +w_n{x}_n)}}$$

4. 模型训练和参数优化

我们以二分类问题为例，假设有一个训练集包含 m 个样本，每个样本有 n 个特征。逻辑回归模型的目标是对样本进行二分类，并输出样本属于正类的概率。

4.1 模型构建

逻辑回归模型通过将线性回归模型的输出应用于逻辑函数（如sigmoid函数）来产生概率输出。模型的输出可以表示为：

$$z=w_0+w_1{x}_1+w_2{x}_2+\dots +w_n{x}_n$$

其中，$w_0,w_1,\dots ,w_n$ 是模型的权重参数，$x_1,x_2,\dots ,x_n$ 是样本的特征值。

应用逻辑函数（sigmoid函数）将线性输出转换为概率值，公式如下：

$$h(z)=\frac{1}{1+e^{-z}}$$

其中，$h(z)$ 表示样本属于正类的概率。

4.2 损失函数

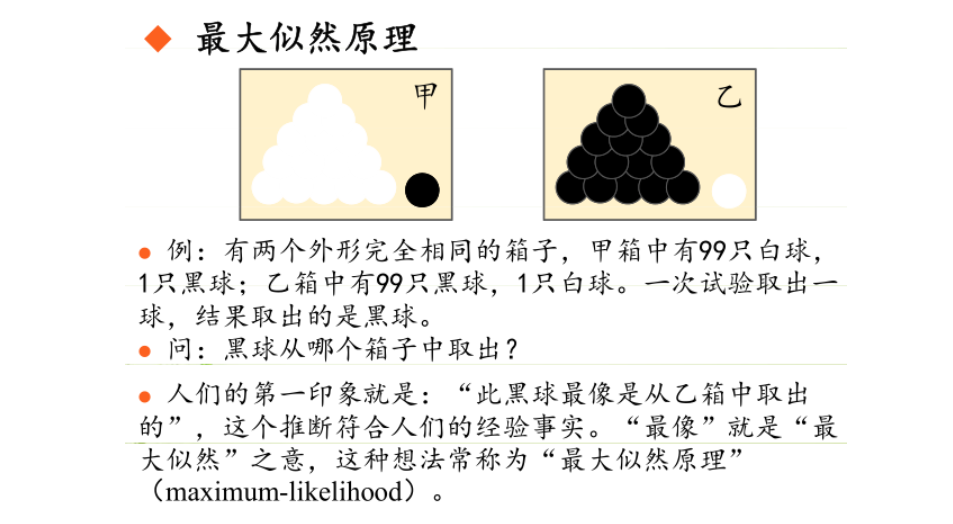
极大似然估计（Maximum Likelihood Estimation，MLE）在逻辑回归模型中通常应用于参数优化的步骤。具体来说，它用于确定逻辑回归模型的权重参数。

为了训练模型，我们需要定义一个损失函数来衡量模型预测值与实际标签之间的差异。在逻辑回归中，通常使用对数损失函数（也被称为二元交叉熵损失函数）作为损失函数。对于一个训练样本 $(x,y)$，其中 $x$ 是特征向量，$y$ 是对应的标签（0或1），对数损失函数的表达式如下：

$$\mathcal{L}(h(x),y)=-y\log (h(x))-(1-y)\log (1-h(x))$$

其中，$h(x)$ 表示样本属于正类的概率，根据模型构建中的逻辑函数（sigmoid函数）计算得到。

极大似然估计的目标是最大化所有训练样本的似然函数（likelihood function）。对于逻辑回归模型，似然函数可以表示为所有样本的条件概率的乘积。假设训练集包含 $m$ 个样本，则似然函数可以表示为：

$$\mathcal{L}(w)=\prod _{i=1}^m(h(x^{(i)}){)}^{y^{(i)}}(1-h(x^{(i)}){)}^{(1-y^{(i)})}$$

其中，$x^{(i)}$ 是第 $i$ 个样本的特征向量，$y^{(i)}$ 是对应的标签。

为了方便计算，通常会取对数似然函数（log-likelihood function）的负值作为损失函数。这样做的好处是将乘法转换为加法，简化了计算。对数似然函数的表达式如下：

$$\mathcal{J}(w)=-\frac{1}{m}\sum _{i=1}^m[y^{(i)}\log (h(x^{(i)}))+(1-y^{(i)})\log (1-h(x^{(i)}))]$$

最终的目标是最小化对数似然损失函数 $\mathcal{J}(w)$。为了实现这一目标，可以使用梯度下降等优化算法来更新权重参数 $w$，使得损失函数逐渐减小。因此，极大似然估计在逻辑回归模型中应用于参数优化的步骤，通过最大化似然函数或最小化对数似然损失函数来确定模型的权重参数。

4.3 参数优化

为了最小化损失函数，我们需要选择适当的优化算法来更新模型的参数。其中最常用的优化算法是梯度下降算法。梯度下降算法根据损失函数的梯度方向来更新模型的参数，使得损失函数逐渐减小。

对于逻辑回归，我们需要计算损失函数对于各个参数的偏导数，然后使用梯度下降算法进行参数更新。对于权重参数 $w_j$，其梯度的计算公式如下：

$$\frac{\partial \mathcal{L}}{\partial w_j}=\frac{1}{m}\sum _{i=1}^m(h(x^{(i)})-y^{(i)})x_j^{(i)}$$

其中，$m$ 是训练样本的数量，$x^{(i)}$ 是第 $i$ 个样本的特征向量，$y^{(i)}$ 是对应的标签。

根据梯度下降算法的更新规则，可以更新权重参数 $w_j$：

$$w_j:=w_j-\alpha \frac{\partial \mathcal{L}}{\partial w_j}$$

其中，$\alpha$ 是学习率，控制参数更新的步长。

4.4 训练过程

在训练过程中，我们将数据集的所有样本输入模型中，计算损失函数，并使用梯度下降算法迭代地更新模型的参数。训练过程通常需要多个迭代周期（epochs），每个周期中数据集的样本都会被使用一次。训练过程中可以监控训练集上的损失值和其他评估指标，以评估模型的性能和收敛情况。

4.5 模型评估

在训练完成后，可以使用独立的验证集或测试集对模型进行评估。常见的评估指标包括准确率、精确率、召回率和 F1 分数等。这些指标可以帮助我们了解模型的分类性能和泛化能力。

在逻辑回归的训练过程中，我们使用最大似然估计来拟合模型参数。最大似然估计的核心思想是选择能够最大化观测数据出现概率的模型参数。

对于逻辑回归模型，我们可以将观测数据的似然函数表示为：

$$L(w)=\prod _{i=1}^{m}P(y^{(i)}=1|x^{(i)}{)}^{y^{(i)}}\cdot (1-P(y^{(i)}=1|x^{(i)})){)}^{1-y^{(i)}}$$

其中，$m$ 是训练样本的数量，$y^{(i)}$ 是第 $i$ 个样本的真实标签，$x^{(i)}$ 是对应的特征向量。

为了方便计算，我们通常将似然函数取对数，得到对数似然函数：

$$\log L(w)=\sum _{i=1}^m[y^{(i)}\log P(y^{(i)}=1|x^{(i)})+(1-y^{(i)})\log (1-P(y^{(i)}=1|x^{(i)}))]$$

我们的目标是最大化对数似然函数，可以通过梯度上升法或优化算法（如牛顿法、拟牛顿法）来求解模型参数 $w$。

5. 多分类问题的处理

逻辑回归不仅适用于二分类问题，还可以通过一些扩展方法处理多分类问题。其中一种常见的方法是“一对多”（One-vs-Rest）策略。对于每个类别，我们训练一个二分类的逻辑回归模型，预测样本是否属于该类别。最终，我们选择概率最高的类别作为预测结果。

下面将详细介绍这种方法的步骤：

假设我们有一个包含 $K$ 个类别的多分类问题，其中每个样本的特征表示为 $x$，目标类别为 $y$，$y\in \{1,2,\dots ,K\}$。现在我们将训练 $K$ 个二分类的逻辑回归模型，每个模型对应一个类别。假设模型 $k$ 对应类别 $k$，我们的目标是训练一个模型来预测样本属于类别 $k$ 的概率。

以下是一对多策略的步骤：

1. 数据准备：首先，我们需要准备训练数据。对于每个类别 $k$，我们将目标类别为 $k$ 的样本标记为正类（1），将目标类别不是 $k$ 的样本标记为负类（0）。

2. 模型训练：对于每个类别 $k$，我们训练一个二分类的逻辑回归模型。在训练阶段，我们使用目标类别为 $k$ 的标签作为正类标签，其他类别的标签作为负类标签。通过最大似然估计或其他优化算法来估计模型参数。

3. 预测过程：对于一个新的样本 $x$，我们将其输入到每个模型中，得到样本属于每个类别的概率。然后，我们选择具有最高概率的类别作为预测结果。

对于多分类问题，逻辑回归可以通过一对多策略进行处理。该策略训练了多个二分类的逻辑回归模型，每个模型对应一个类别。在预测阶段，选择具有最高概率的类别作为预测结果。这种一对多策略的优点是简单且易于理解。然而，它可能存在类别不平衡的问题，即某些类别的样本数量较少，导致模型在这些类别上的性能较差。在处理类别不平衡问题时，可以使用权重调整、过采样或欠采样等技术来改善模型的性能。

除了一对多策略，还有其他处理多分类问题的方法，例如多项式逻辑回归、softmax回归等。这些方法在逻辑回归的基础上进行扩展，可以更好地处理多分类问题。

6. 应用和总结

逻辑回归在实际应用中具有广泛的应用。它被用于医学、金融、市场营销等领域。例如，在医学领域，逻辑回归可以用于预测患者是否患有某种疾病，从而帮助医生进行诊断和治疗决策。

逻辑回归是一种基于线性回归的分类算法，通过引入逻辑函数将线性回归的输出转换为概率值。它通过最大似然估计和梯度下降等优化算法来拟合模型并进行分类预测。逻辑回归在分类问题中具有广泛的应用，并且可以通过一对多策略扩展到多分类问题。

通过本文的介绍，我们深入理解了逻辑回归的原理和应用。逻辑回归是机器学习中的重要工具之一，希望本文能够帮助您更好地理解和应用逻辑回归算法。如果您对逻辑回归还有更多的疑问或者想要进一步学习，可以深入探索相关的教材和资源。祝您在机器学习的旅程中取得成功！