决策树

# 决策树

决策树是一种树状结构，用于对数据集进行分类或回归。每个内部节点代表一个特征或属性，每个叶子节点代表一个类别或数值输出。通过从根节点开始，沿着树的分支逐步进行决策，最终到达叶子节点以获得预测结果。

例如：

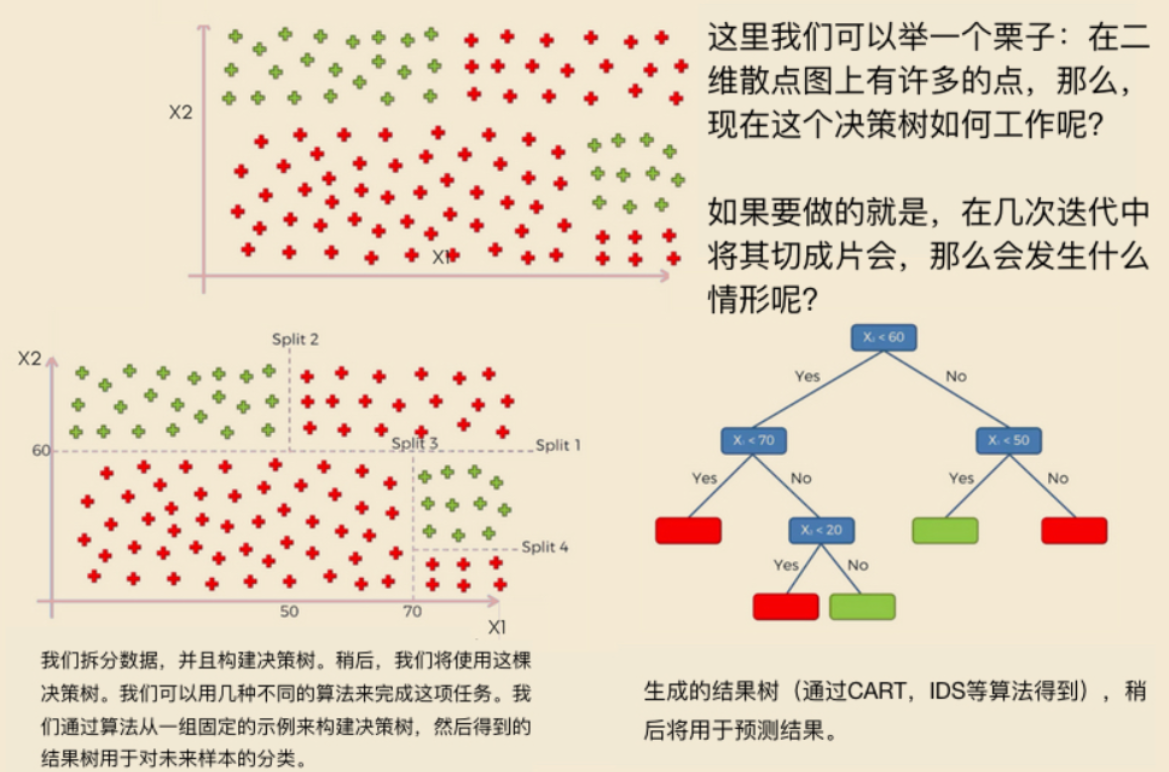
# 决策树如何工作？

决策树通过递归地将数据分割成基于输入特征的子集来工作。树中的每个内部节点表示一个特征或属性，每个叶节点表示一个类标签或预测值。

决策树算法的工作过程如下：

根节点：算法从整个数据集开始作为根节点。
分割：算法选择最佳的特征来分割数据基于某个标准，如信息增益或 Gini 不纯度。
子节点：算法为每个分割创建子节点，并递归地将同样的过程应用于每个子节点。
叶节点：算法停止时所有实例在一个节点中都属于同一个类或达到停止标准。

在决策树中选择根节点（或任何节点）的分类条件基于一个关键概念，即信息增益。信息增益衡量的是在给定一个特征进行分类后，目标变量的不确定性减少的程度。这个减少的不确定性通常通过信息熵来计算。

# 信息熵的概念

信息熵是一个衡量数据集混乱程度的指标。在决策树中，它用来衡量在没有任何额外信息的情况下，预测结果（分类标签）所需的信息量。熵值越高，数据的不确定性和混乱程度越大，相应地，数据的信息内容也越丰富。公式如下：

H (S) = - \sum_{x \in X} p (x) \log_{2} p (x)

其中 $p (x)$ 是选择该分类的概率。

例如上图中的分类结果是“红点”还是“绿点”的信息熵，其中假如红色点有48个，绿色点有36，让我们计算上图中的分类列的信息熵：

p (红点) = \frac{48}{48 + 36} = \frac{48}{84} = 0.5714

p (绿点) = \frac{36}{48 + 36} = \frac{36}{84} = 0.4286

现在，我们可以使用公式计算信息熵，将值代入，我们得到：

H (S) = - [0.5714 \log_{2} 0.5714 + 0.4286 \log_{2} 0.4286] \approx 0.9544

所以，这个分类列的信息熵约为 0.9544。

通过以上计算可以得到，某个类别下信息量越多，熵越大，信息量越少，熵越小。假设这个信息类别只有红点或者绿点，那么这列的信息熵为0，自己可验算。

# 条件熵

当考虑某个特征（如年龄、收入层次等）作为决策树的节点时，==我们计算的是给定该特征后，目标变量的条件熵==，表示为 $H (S | X)$ 。条件熵衡量了在已知某个特征的情况下，目标变量的熵，也就是剩余的不确定性。公式如下：

H (S | X) = \sum_{x \in X} p (x) H (S | x)

其中 $H (S | x)$ 是在特征 $X$ 的特定值 $x$ 下的目标变量的熵，而 $p (x)$ 是特征 $X$ 取值 $x$ 的概率。

# 信息增益

信息增益是原始数据熵与条件熵之差，用来评估使用该特征进行分割后不确定性减少的程度。公式如下：

Information Gain = H (S) - H (S | X)

信息增益越大，意味着使用该特征作为分割点后，数据集的熵减少得越多，也就是说，分类后的纯度提高了，因此分类更彻底。

# 为什么熵越低分类越彻底

熵越低意味着数据集中的不确定性越小，结果的可预测性越高。例如，如果一个数据集中所有的实例都属于同一个类别，则该数据集的熵为0，因为没有任何不确定性或混乱——我们可以完美地预测每个实例的类别。因此，在决策树构建过程中，我们寻找那些能最大化信息增益（即最大程度降低熵）的特征，以便更有效地分类数据，提高决策树的预测精度。

通过这种方式，我们能够确定应该使用哪个特征作为决策树的节点，从而有效地将数据分组，使每个子组在目标变量上尽可能地“纯净”，简化后续的分类任务。

让我们通过一个简单的例子来解释如何使用信息熵和信息增益来选择决策树中的根节点。假设我们有以下数据集，其中包括四个特征：年龄（Age）、收入层次（Income Level）、是否学生（Student）、信用等级（Credit Rating）；目标变量是“是否购买电脑”（Buy Computer）。

假设数据集如下：

Age	Income Level	Student	Credit Rating	Buy Computer
Young	High	No	Fair	No
Young	High	No	Excellent	No
Middle	High	No	Fair	Yes
Senior	Medium	No	Fair	Yes
Senior	Low	Yes	Fair	Yes
Senior	Low	Yes	Excellent	No
Middle	Low	Yes	Excellent	Yes
Young	Medium	No	Fair	No
Young	Low	Yes	Fair	Yes
Senior	Medium	Yes	Fair	Yes
Young	Medium	Yes	Excellent	Yes
Middle	Medium	No	Excellent	Yes
Middle	High	Yes	Fair	Yes
Senior	Medium	No	Excellent	No

# 步骤 1: 计算总体熵

首先，计算目标变量“是否购买电脑”在整个数据集中的熵。假设有9个“是”（Yes）和5个“否”（No）。

\begin{aligned} H (B u y C o m p u t e r) & = - (\frac{9}{14} \log_{2} \frac{9}{14} + \frac{5}{14} \log_{2} \frac{5}{14}) \\ = - (0.643 \log_{2} 0.643 + 0.357 \log_{2} 0.357) \\ \approx 0.940 \end{aligned}

# 步骤 2: 计算条件熵（以“学生”为例）

接下来，看看“是否学生”这一特征的条件熵：

Student	Buy Computer	Count
Yes	Yes	6
Yes	No	1
No	Yes	3
No	No	4

\begin{aligned} H (B u y C o m p u t e r | S t u d e n t) & = \frac{7}{14} (- (\frac{6}{7} \log_{2} \frac{6}{7} + \frac{1}{7} \log_{2} \frac{1}{7})) + \frac{7}{14} (- (\frac{3}{7} \log_{2} \frac{3}{7} + \frac{4}{7} \log_{2} \frac{4}{7})) \\ \approx 0.863 \end{aligned}

# 步骤 3: 计算信息增益

\begin{aligned} Information Gain & = H (B u y C o m p u t e r) - H (B u y C o m p u t e r | S t u d e n t) \\ = 0.940 - 0.863 = 0.077 \end{aligned}

我们会对每个特征重复上述计算过程，然后选择信息增益最大的特征作为决策节点。在这个例子中，如果“是否学生”具有最高的信息增益，它将被选为根节点（或当前节点）。这种方式确保了每次分割都尽可能地降低了数据集的不确定性，从而使得子集更加纯净，便于进一步分类。

决策树预剪枝和后剪枝

决策树对训练集有很好的分类能力，但是对于未知的测试集未必有好的分类能力，导致模型的泛化能力弱，可能发生过拟合问题。为了防止过拟合问题的出现，可以对决策树进行剪枝。剪枝分为预剪枝和后剪枝。

预剪枝。预剪枝就是在构建决策树的时候提前停止。例如，指定树的深度最大为5，那么训练出来决策树的高度就是5。预剪枝主要是建立某些规则限制决策树的生长，降低了过拟合的风险，降低了建树的时间，但是有可能带来欠拟合问题。

后剪枝。后剪枝是一种全局的优化方法，在决策树构建好之后，然后才开始进行剪枝。后剪枝的过程就是删除一些子树，这个叶子节点的标识类别通过大多数原则来确定，即属于这个叶子节点下大多数样本所属的类别就是该叶子节点的标识。选择减掉哪些子树时，可以计算没有减掉子树之前的误差和减掉子树之后的误差，如果相差不大，可以将子树减掉。一般使用后剪枝得到的结果比较好。

后剪枝的优点是可以避免过拟合问题，并且可以提高模型的泛化能力。但是，后剪枝也存在一些缺点，例如计算复杂度高，需要大量的计算资源。因此，在实际应用中，需要根据具体情况选择合适的剪枝方法。

# 代码实现

# 步骤 1: 引入必要的库

首先，让我们引入必要的Python库，这些库将在整个代码中使用。

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd

1
2
3

# 步骤2：导入数据集

在这一步，我们将导入我们的数据集，该数据集位于文件"Social_Network_Ads.csv"中。数据集通常包含了特征（features）和目标变量（target variable）。你可以在Social_Network_Ads.csv下载数据集。

这个数据集看起来像这样：

Age	EstimatedSalary	Purchased
19	19000	0
35	20000	0
...	...	...

我们的目标是根据年龄（Age）和估计工资（EstimatedSalary）来预测用户是否购买了某个产品（Purchased）。我们将数据集拆分为特征（X）和目标变量（y）。

# 导入数据集
dataset = pd.read_csv('../data/Social_Network_Ads.csv')
X = dataset.iloc[:, [2, 3]].values
y = dataset.iloc[:, 4].values

1
2
3
4

# 步骤 3: 数据预处理

# 3.1数据拆分

在这一步骤中，我们将数据集分为两个部分：训练集和测试集。

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=0)

1
2

train_test_split：这是Scikit-Learn库的函数，用于将数据集拆分为训练集和测试集。test_size 参数设置了测试集的比例。

# 3.2特征缩放

特征缩放是将特征的值缩放到相同的尺度范围，以确保模型的性能不会受到不同尺度特征的影响。

from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
X_train = sc.fit_transform(X_train)
X_test = sc.transform(X_test)

1
2
3
4

StandardScaler：这是Scikit-Learn库的标准化类，用于将特征标准化为均值为0、方差为1的正态分布。

# 步骤 4: 构建决策树分类器

在这一步骤中，我们构建了一个决策树分类器模型。

from sklearn.tree import DecisionTreeClassifier
classifier = DecisionTreeClassifier(criterion='entropy', random_state=0)
classifier.fit(X_train, y_train)

1
2
3

DecisionTreeClassifier：这是Scikit-Learn库的决策树分类器类，用于构建决策树模型。
criterion='entropy'：我们选择使用熵（entropy）作为分裂标准，用于测量节点的不纯度。
random_state=0：这个参数用于控制模型中的随机性，设置为0可以使结果可重复。

这些是代码中的关键步骤和方法，希望这些解释有助于你理解它们的作用和使用。接下来，我们将继续执行模型评估和结果可视化的步骤。

# 步骤5：模型预测

我们使用训练好的SVM模型对测试集进行预测。

# 在测试集上进行预测
y_pred = classifier.predict(X_test)

1
2

# 步骤6：评估模型性能

在这一步中，我们评估了SVM模型的性能，了解模型的准确性和其他性能指标。我们使用了混淆矩阵和分类报告来完成这项任务。

# 6.1 混淆矩阵（Confusion Matrix）

cm = confusion_matrix(y_test, y_pred)
print("混淆矩阵:")
print(cm)

1
2
3

confusion_matrix 函数接受两个参数：真实的目标值 y_test 和模型预测的目标值 y_pred。
混淆矩阵是一个二维数组，它展示了模型的分类性能。它的四个元素分别是真正例（True Positives，TP）、真负例（True Negatives，TN）、假正例（False Positives，FP）和假负例（False Negatives，FN）的数量。这些元素用于计算精确度、召回率等性能指标。

# 6.2 分类报告（Classification Report）

print("\n分类报告:")
print(classification_report(y_test, y_pred))

1
2

classification_report 函数接受两个参数：真实的目标值 y_test 和模型预测的目标值 y_pred。
分类报告提供了关于模型性能的详细信息，包括精确度（Precision）、召回率（Recall）、F1分数（F1-score）等。它对每个类别进行了单独的评估，并提供了加权平均值（weighted average）。

这些方法和参数是评估分类模型性能时常用的工具，可以帮助我们理解模型的强项和弱项，以便进一步优化和改进模型。

混淆矩阵:
[[62  6]
 [ 3 29]]
分类报告:
              precision    recall  f1-score   support
           0       0.95      0.91      0.93        68
           1       0.83      0.91      0.87        32
    accuracy                           0.91       100
   macro avg       0.89      0.91      0.90       100
weighted avg       0.91      0.91      0.91       100

1
2
3
4
5
6
7
8
9
10

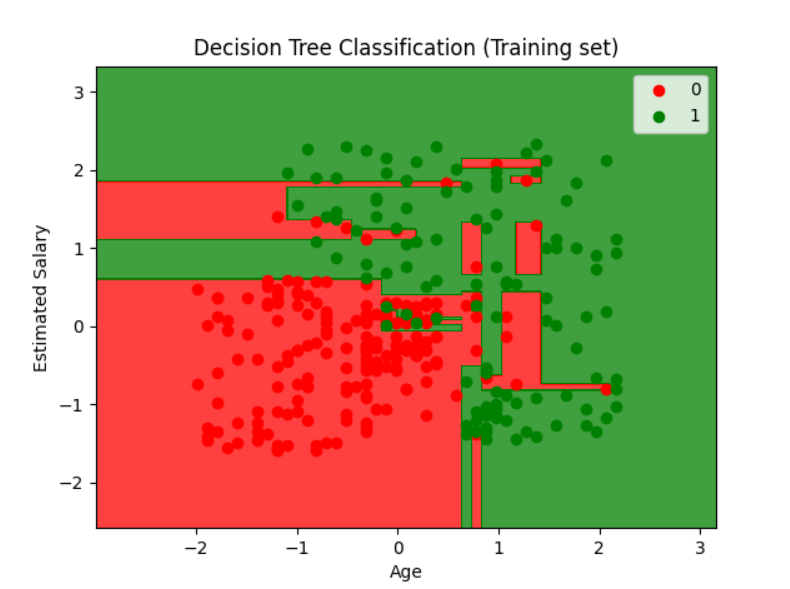
# 步骤7：可视化结果

# Visualising the Training set results
from matplotlib.colors import ListedColormap
X_set, y_set = X_train, y_train
X1, X2 = np.meshgrid(np.arange(start=X_set[:, 0].min() - 1, stop=X_set[:, 0].max() + 1, step=0.01),
                     np.arange(start=X_set[:, 1].min() - 1, stop=X_set[:, 1].max() + 1, step=0.01))
plt.contourf(X1, X2, classifier.predict(np.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape),
             alpha=0.75, cmap=ListedColormap(['red', 'green']))
plt.xlim(X1.min(), X1.max())
plt.ylim(X2.min(), X2.max())
for i, j in enumerate(np.unique(y_set)):
    plt.scatter(X_set[y_set == j, 0], X_set[y_set == j, 1],
                c=['red', 'green'][i], label=j)
plt.title('Decision Tree Classification (Training set)')
plt.xlabel('Age')
plt.ylabel('Estimated Salary')
plt.legend()
plt.show()

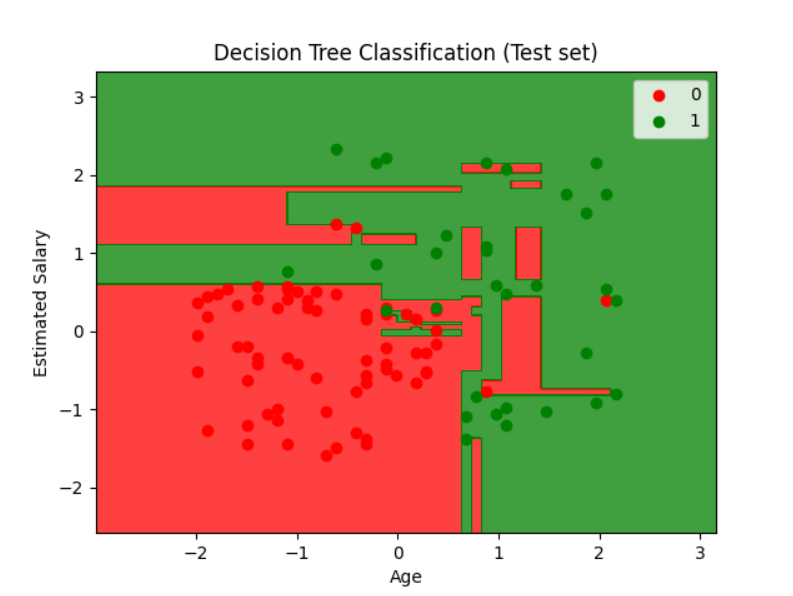
# Visualising the Test set results
from matplotlib.colors import ListedColormap
X_set, y_set = X_test, y_test
X1, X2 = np.meshgrid(np.arange(start=X_set[:, 0].min() - 1, stop=X_set[:, 0].max() + 1, step=0.01),
                     np.arange(start=X_set[:, 1].min() - 1, stop=X_set[:, 1].max() + 1, step=0.01))
plt.contourf(X1, X2, classifier.predict(np.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape),
             alpha=0.75, cmap=ListedColormap(['red', 'green']))
plt.xlim(X1.min(), X1.max())
plt.ylim(X2.min(), X2.max())
for i, j in enumerate(np.unique(y_set)):
    plt.scatter(X_set[y_set == j, 0], X_set[y_set == j, 1],
                c=['red', 'green'][i], label=j)
plt.title('Decision Tree Classification (Test set)')
plt.xlabel('Age')
plt.ylabel('Estimated Salary')
plt.legend()
plt.show()

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

编辑

上次更新: 2025/04/01, 01:48:12

← 使用SVM进行二分类随机森林→