支持向量机（SVM)

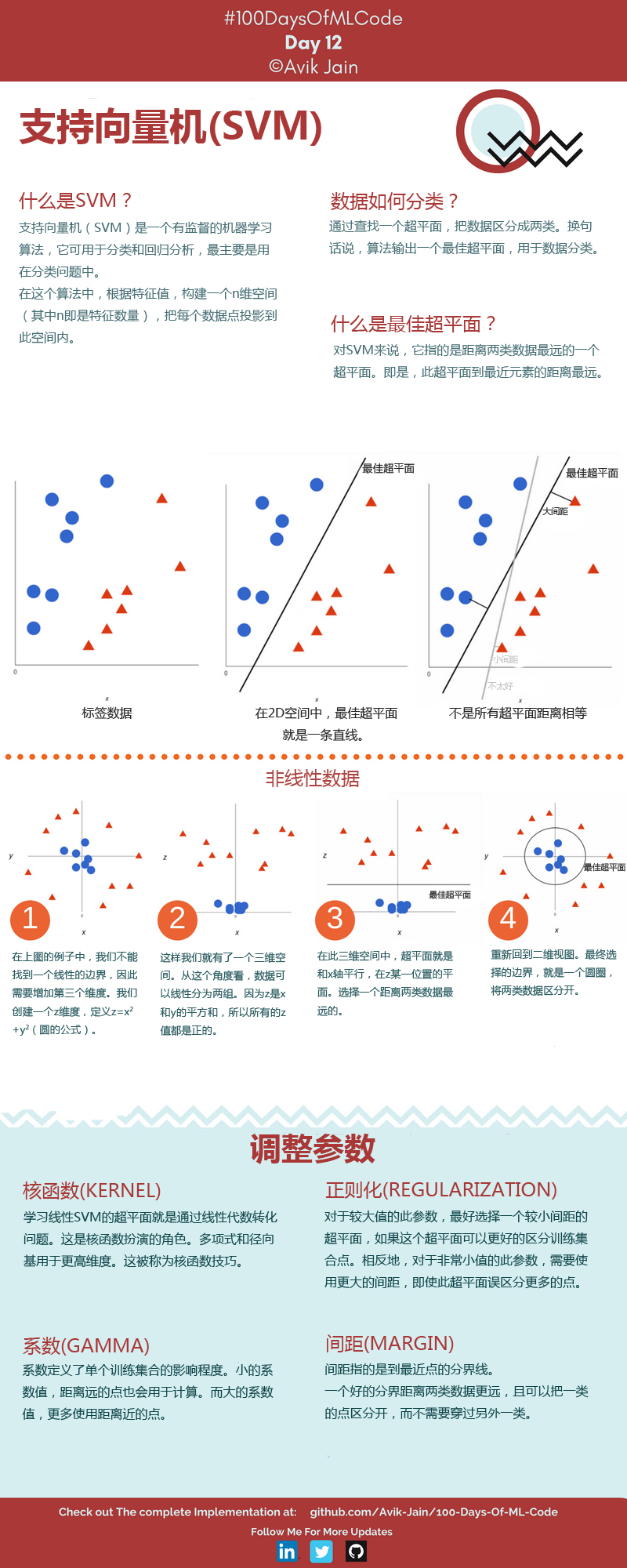
理解支持向量机（Support Vector Machine，简称SVM）的原理对于深入了解这一强大的机器学习算法至关重要。SVM是一种用于分类和回归的监督学习方法，它在许多领域都有广泛的应用，包括文本分类、图像分类、生物信息学等。在本文中，我们将深入研究SVM的原理，包括其核心概念、数学基础和工作原理。

# 支持向量机的基本概念

# 核心思想

支持向量机是一种二元线性分类器，其核心思想是找到一个最优的超平面，将不同类别的数据点分开，并且在超平面两侧有足够的间隔（margin），以提高分类的鲁棒性。这个最优的超平面被称为“决策边界”。

# 1. 超平面

在线性代数和几何学中，超平面是一个重要的概念，特别在支持向量机（SVM）和其他机器学习算法中经常被提到。超平面是一个在n维空间中的（n-1）维子空间，通常用于将n维空间中的数据点分为两个不同的类别或集合。

更具体地说，对于n维空间（通常是欧几里得空间），一个超平面可以由一个线性方程表示，其一般形式为：

a_{1} x_{1} + a_{2} x_{2} + \dots + a_{n} x_{n} = b

其中， $(a_{1}, a_{2}, \dots, a_{n})$ 是超平面的法向量（normal vector），决定了超平面的方向， $b$ 是截距（intercept）。这个超平面将n维空间分为两个半空间：一个半空间包含所有满足上述线性方程的点，另一个半空间包含所有不满足该方程的点。

在2D空间（平面）中，超平面是一条直线。在3D空间中，超平面是一个平面。在更高维度的空间中，超平面仍然是一个（n-1）维的线性子空间。

在机器学习中，超平面经常用于将数据点分为两个不同的类别，例如，通过超平面可以将一个点云分为两个具有不同性质的部分。在支持向量机（SVM）中，超平面是用来构建决策边界的关键概念。 SVM的目标是找到一个最优的超平面，以最大化分类问题的间隔边界，从而提高分类的鲁棒性。

# 2. 支持向量

支持向量是离超平面最近的数据点，它们在分类中起到关键作用。这些数据点用于定义间隔边界，即最靠近超平面的数据点决定了边界的位置。

具体来说，支持向量是满足以下条件的训练数据点：

支持向量属于训练数据集中的特定类别。
支持向量距离超平面（决策边界）最近，也就是离间隔边界最近。

在SVM中，这些支持向量对于确定超平面的位置非常重要，因为它们决定了超平面的位置以及间隔边界的大小。更具体地说，支持向量的法向量（垂直于超平面的向量）与超平面之间的距离是间隔边界的一半。

SVM的训练过程旨在找到最佳的超平面，以便最大化支持向量到超平面的距离，从而使分类问题更加鲁棒。这种间隔的最大化有助于提高SVM的泛化能力，使其在新数据上的表现更好。

总之，支持向量是SVM中最接近决策边界且对决策边界具有重要影响的训练数据点。它们在SVM的训练和分类过程中起到关键作用，帮助确定最优的超平面以实现高效的分类。

# SVM的数学基础

为了更深入地理解SVM，让我们来看一下它的数学基础。在这里，我们将探讨SVM的数学表达式、优化目标和拉格朗日对偶性。

# 1. SVM的数学表达式

SVM的分类问题可以用以下数学表达式来表示：

min_{w, b} \frac{1}{2} | | w | |^{2}

subject to y_{i} (w \cdot x_{i} + b) \geq 1, for i = 1, 2, \dots, N

在这里， $w$ 和 $b$ 是要学习的参数， $x_{i}$ 是输入数据点， $y_{i}$ 是对应的类别标签（通常为+1或-1）， $N$ 是数据点的数量。第一个优化目标是最小化权重向量 $w$ 的范数，以确保找到最优的超平面。第二个公式是约束条件，确保每个数据点都被正确分类并且距离超平面至少为1。

# 2. 优化目标

SVM的优化目标是找到一个能够最大化间隔边界的超平面。这可以通过最小化目标函数中的权重向量 $w$ 的范数来实现。最终的目标是使得数据点距离决策边界的间隔尽可能大。

# 3. 拉格朗日对偶性

SVM问题的优化可以通过拉格朗日对偶性来解决。通过引入拉格朗日乘子，可以将原始问题转化为一个对偶问题，从而更容易解决。拉格朗日对偶性帮助我们找到最优的权重向量 $w$ 和截距 $b$ 。

拉格朗日对偶性是解决支持向量机（Support Vector Machine，SVM）优化问题的关键数学概念。它将原始的非凸优化问题转化为一个对偶问题，从而更容易求解。在了解拉格朗日对偶性的具体内容之前，让我们回顾一下SVM的优化问题。

# SVM的优化问题回顾

SVM的原始优化问题可以表示为：

最小化目标函数：

min_{w, b} \frac{1}{2} | | w | |^{2}

约束条件：

y_{i} (w \cdot x_{i} + b) \geq 1, 对于 i = 1, 2, \dots, N

这里， $w$ 是超平面的权重向量， $b$ 是截距， $x_{i}$ 是训练数据点的特征向量， $y_{i}$ 是对应的类别标签（+1 或 -1）， $N$ 是训练样本数量。

原始问题的目标是最小化权重向量 $w$ 的范数，同时确保数据点距离超平面至少为1。这是一个凸优化问题，但在某些情况下，它可能不太容易求解。为了解决这个问题，我们引入了拉格朗日乘子，将其转化为对偶问题。

# 拉格朗日对偶性

拉格朗日对偶性的核心思想是将原始问题中的约束条件引入到目标函数中，通过引入拉格朗日乘子来实现。对于SVM问题，我们引入拉格朗日乘子 $α_{i}$ ，对应于每个约束条件。然后，我们构建拉格朗日函数（Lagrangian）如下：

# 求解对偶问题

通过求解对偶问题，我们可以找到最优的拉格朗日乘子 $α$ ，并通过它们来找到最优的权重向量 $w$ 和截距 $b$ 。这些最优的参数将定义SVM的最佳超平面。

对偶问题的解决通常涉及到数学优化技术，如凸优化或二次规划。一旦找到了最优的 $α$ ，我们可以使用它们来计算 $w$ 和 $b$ 。

拉格朗日对偶性是解决SVM优化问题的关键概念。它将原始问题转化为对偶问题，使得求解变得更加容易，并且保持了问题的凸性质。通过引入拉格朗日乘子，我们可以最大化拉格朗日函数关于乘子 $α$ 的下界，从而找到最优的参数，进而定义SVM的最佳超平面。这种数学技巧使得SVM成为了一个强大的分类算法，可以有效地处理各种机器学习问题。

# SVM的工作原理

现在让我们来深入了解SVM是如何工作的，包括训练过程和预测过程。

# 1. 训练过程

SVM的训练过程可以分为以下步骤：

# a. 数据准备

首先，收集和准备带有标签的训练数据集。每个数据点都有一个特征向量 $x_{i}$ 和对应的类别标签 $y_{i}$ 。

# b. 构建优化问题

将SVM的优化问题构建为前面提到的形式，即找到一个最优的超平面，以最大化间隔边界并确保数据点的正确分类。

# c. 求解优化问题

使用数学优化技术，如拉格朗日乘子法，来求解优化问题，找到最优的权重向量 $w$ 和截距 $b$ 。

# d. 决策边界

根据找到的最优权重向量 $w$ 和截距 $b$ ，构建决策边界，用于将新的数据点进行分类。

# 2. 预测过程

一旦训练完成，就可以使用SVM来进行新数据点的分类。预测过程包括以下步骤：

# a. 特征提取

对新的输入数据进行特征提取，得到特征向量 $x$ 。

# b. 计算决策函数

使用训练好的权重向量 $w$ 和截距 $b$ ，计算决策函数 $f (x) = w \cdot x + b$ 。

# c. 判定类别

根据决策函数的结果，如果 $f (x) > 0$ ，则将数据点分类为正类别；如果 $f (x) < 0$ ，则将数据点分类为负类别。

# SVM的核函数

SVM还可以使用核函数来处理非线性分类问题。核函数允许SVM在高维空间中进行非线性映射，从而将非线性问题转化为线性问题。一些常见的核函数包括

线性核、多项式核和径向基函数（RBF）核。

# 总结

支持向量机是一种强大的机器学习算法，它在分类和回归问题中都有广泛的应用。通过找到最优的超平面并最大化间隔边界，SVM能够提供高度鲁棒的分类性能。此外，SVM还可以通过核函数处理非线性问题，扩展了其应用领域。深入理解SVM的原理和数学基础是使用它的关键，它可以帮助您更好地理解和应用这一强大的机器学习算法。

编辑

#机器学习 #SVM

上次更新: 2025/04/01, 01:48:12

← k最近邻分类任务代码演示使用SVM进行二分类→