多元线性回归

提示

多元线性回归是一种机器学习技术，用于建模和预测多个自变量与一个因变量之间的关系。它建立了一个线性函数，通过拟合训练数据来预测未知数据的因变量。多元线性回归适用于处理多个特征（维度）之间的复杂关系。我们将使用来自50个创业公司的数据集进行示范，并使用matplotlib库可视化结果。

数据集下载

点击此处下载数据50_Startups.csv

这个数据集包含了50个初创公司的相关数据，包括研发支出（R&D Spend）、管理费用（Administration）、市场营销支出（Marketing Spend）、所在州（State）和利润（Profit）。通过对这些数据进行分析，可以得出一些有关这些初创公司的洞察。我们可以绘制各个特征与利润之间的散点图，以便直观地观察它们之间的关系。这可能揭示出一些趋势或模式，例如是否存在线性关系或非线性关系。

1. 导入库和数据

首先，我们需要导入所需的库，并加载我们的数据集。

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import LabelEncoder, OneHotEncoder

# 导入数据
dataset = pd.read_csv('../data/50_Startups.csv')
X = dataset.iloc[:, :-1].values
Y = dataset.iloc[:, -1].values

在上述代码中，我们导入了必要的库，并使用pandas库加载了一个名为50_Startups.csv的数据集。我们将自变量存储在X中，将因变量存储在Y中。

2. 数据预处理

在数据预处理中，我们通常需要将文本数据转换为机器学习算法可以处理的数值形式。Label编码器是一种常用的转换工具，它将每个类别映射到唯一的整数标签。例如，"New York"可能被编码为0，"California"可能被编码为1，"Florida"可能被编码为2。

label_encoder_X = LabelEncoder()
X[:, 3] = label_encoder_X.fit_transform(X[:, 3])

然而，这样的编码方式可能会引入一种错误的排序关系。例如，如果我们将这些整数标签直接输入到机器学习算法中，算法可能会错误地认为0 < 1 < 2，从而导致错误的结果。

为了避免这个问题，我们使用One-Hot编码器进一步转换标签编码后的数据。One-Hot编码器将每个整数标签表示为一个二进制向量，其中只有一个元素为1，其余元素为0。例如，"New York"将被编码为[1, 0, 0]，"California"将被编码为[0, 1, 0]，"Florida"将被编码为[0, 0, 1]。

这种表示方式消除了任何可能的排序关系，同时保留了类别之间的独立性。机器学习算法可以更好地理解和处理这种二进制形式的数据。

onehot_encoder = OneHotEncoder(categories='auto', drop='first')
X_encoded = onehot_encoder.fit_transform(X[:, 3].reshape(-1, 1)).toarray()
X = np.concatenate((X[:, :3], X_encoded, X[:, 4:]), axis=1)

在上述代码中，我们使用LabelEncoder对第3列进行编码，将文本数据转换为数字。然后，我们使用OneHotEncoder对编码后的数据进行独热编码，并将结果拼接回原始特征矩阵中。在避免虚拟变量陷阱时，我们应该使用 OneHotEncoder 的 drop='first' 参数来指定在独热编码时丢弃第一个虚拟变量。

为什么要指定在独热编码时丢弃第一个虚拟变量？
假设我们有一个特征"颜色"，它有三个类别：红色、绿色和蓝色。我们想要对该特征进行独热编码，以便在模型中使用。

在传统的独热编码中，我们会创建三个虚拟变量列，分别表示红色、绿色和蓝色。这样，如果一个样本是红色，那么红色虚拟变量将为1，而绿色和蓝色虚拟变量将为0。同样，对于绿色和蓝色样本，相应的虚拟变量将为1，其他虚拟变量为0。

然而，为了避免虚拟变量陷阱，我们需要删除一个虚拟变量列。在这种情况下，我们可以选择删除红色虚拟变量列。这是因为如果绿色和蓝色虚拟变量都为0，则可以确定样本的颜色是红色。

下面是独热编码后的示例：

颜色	绿色	蓝色
红色	0	0
绿色	1	0
蓝色	0	1

在这个示例中，我们只使用了两列虚拟变量来表示三个类别，避免了虚拟变量陷阱。这可以确保特征之间不存在完全的线性相关性，并且模型可以准确估计每个虚拟变量的系数。

3. 划分训练集和测试集

为了评估模型的性能，我们需要将数据集划分为训练集和测试集。我们使用train_test_split函数来实现这一步骤。

X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.2, random_state=0)

在上述代码中，我们将数据集划分为80%的训练集和20%的测试集。X_train和Y_train包含训练数据，X_test和Y_test包含测试数据。

4. 训练模型

接下来，我们使用训练集数据来训练多元线性回归模型。

from sklearn.linear_model import LinearRegression

regressor = LinearRegression()
regressor = regressor.fit(X_train, Y_train)

在上述代码中，我们导入LinearRegression类，并创建了一个regressor对象。然后，我们使用训练集数据来拟合（训练）模型。

5. 进行预测

训练完成后，我们可以使用测试集数据进行预测。

y_pred = regressor.predict(X_test)

在上述代码中，我们使用训练好的模型regressor对测试集数据进行预测，并将预测结果存储在变量y_pred中。

6. 可视化结果

最后，我们可以使用matplotlib库将训练集和测试集的结果可视化，以便更好地理解模型的拟合情况。

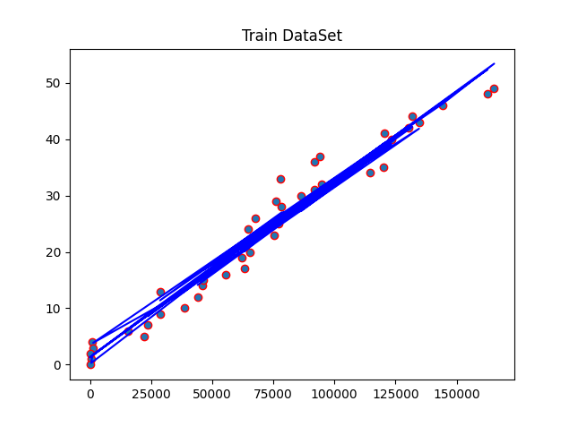
6.1 训练集结果可视化

下面的代码将训练集的散点图和回归线进行可视化。

plt.scatter(X_train[:, 0], Y_train, edgecolors='red')  # 选择第一个特征 X1
plt.plot(X_train[:, 0], regressor.predict(X_train), color='blue')  # 绘制回归线
plt.title("Train DataSet")
plt.show()

在上述代码中，我们使用plt.scatter函数绘制训练集的散点图，其中选择了第一个特征X1作为X轴，因为要保持X轴和Y轴的维度一致才能画图。然后，我们使用plt.plot函数绘制回归线，其中X轴为训练集的第一个特征X1，Y轴为模型对训练集数据的预测结果。最后，我们使用plt.title函数设置图表的标题，并使用plt.show函数显示图表。

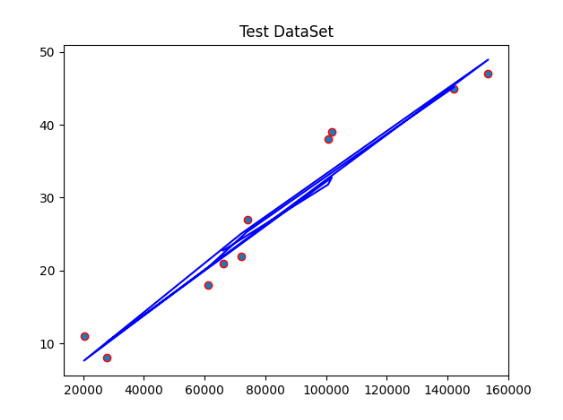
6.2 测试集结果可视化

下面的代码将测试集的散点图和回归线进行可视化。

plt.scatter(X_test[:, 0], Y_test, edgecolors='red')  # 选择第一个特征 X1
plt.plot(X_test[:, 0], regressor.predict(X_test), color='blue')  # 绘制回归线
plt.title("Test DataSet")
plt.show()

在上述代码中，我们使用plt.scatter函数绘制测试集的散点图，其中选择了第一个特征X1作为X轴。然后，我们使用plt.plot函数绘制回归线，其中X轴为测试集的第一个特征X1，Y轴为模型对测试集数据的预测结果。最后，我们使用plt.title函数设置图表的标题，并使用plt.show函数显示图表。