CKKS EXPLAINED: PART 1, VANILLA ENCODING AND DECODING

Introduction

同态加密是一个有前途的领域，它允许在加密数据上进行计算。一篇名为“同态加密是什么”的博文提供了广泛的解释，说明了同态加密的含义以及这一研究领域的重要性。

在本系列文章中，我们将深入研究 Cheon-Kim-Kim-Song (CKKS) 方案，该方案首次在论文《用于近似数算术的同态加密》中进行了讨论。==CKKS 允许我们在复数值向量上进行计算（因此也包括实数值）==。我们的目标是使用 Python 从头开始实现 CKKS，然后通过使用这些密码学原语，探索如何执行复杂操作，比如线性回归、神经网络等等。

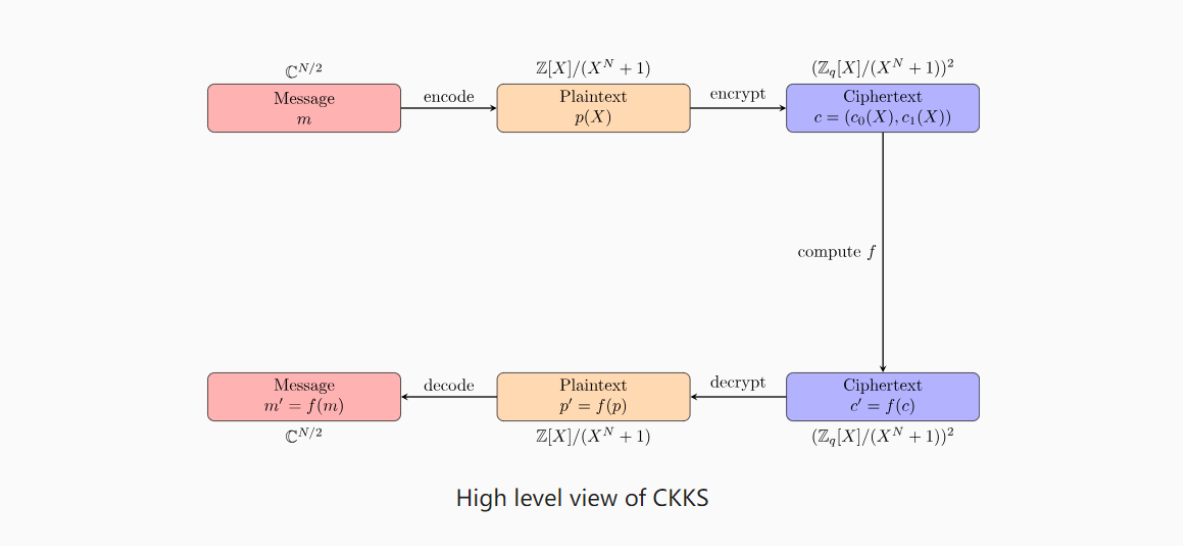
上图提供了 CKKS 的高层视图。我们可以看到，一个消息$m$，即我们想要进行某些计算的值向量，首先被编码成一个明文多项式$p(X)$，然后使用公钥进行加密。

CKKS 使用多项式进行操作，因为与向量上的标准计算相比，它们在安全性和效率之间提供了很好的折衷。

一旦消息$m$被加密为$c$，即一对多项式，CKKS 提供了几种可以在其上执行的操作，例如加法、乘法和旋转。

如果我们用$f$表示一个函数，它是同态操作的组合，那么用秘密密钥解密$c^{\prime }=f(c)$将产生$p^{\prime }=f(p)$。因此，一旦解码，我们将得到$m=f(m)$。

实现同态加密方案的核心思想是在编码器、解码器、加密器和解密器上具有同态属性。这样，密文上的操作将被正确地解密和解码，并且提供的输出就像直接在明文上进行操作一样。

因此，在本文中，我们将看到如何实现编码器和解码器，而在后续文章中，我们将继续实现加密器和解密器，以构建一个同态加密方案。

相关知识：

分圆多项式

在数学中，对于任意正整数$n$，第$n$个分圆多项式是满足以下条件的唯一不可约多项式：

1. 它具有整数系数；
2. 它是多项式$x^n-1$的因式，但不是$x^k-1$的因式，其中$k<n$；
3. 它的根是所有与$n$互质的正整数$k$所对应的第$n$个原始单位根$e^{2i\pi \frac{k}{n}}$。

换句话说，第$n$个分圆多项式可以表示为：

$${\mathrm{\Phi }}_n(x)=\prod _{\begin{array}{c}1\le k\le n\\ gcd(k,n)=1\end{array}}(x-e^{2i\pi \frac{k}{n}})$$

这个多项式也可以定义为具有整数系数的首一多项式（最高次项的系数为1），它是有理数域上任意一个原始$n$次单位根的最小多项式。一个重要的关系是：

$$\prod _{d|n}{\mathrm{\Phi }}_d(x)=x^n-1$$

这表明如果$x$是$x^n-1$的根，那么它就是某个能整除$n$的$d$次原始单位根的根。

这些公式描述了分圆多项式的形式，具体如下：

1. 如果$n$是一个素数，分圆多项式${\mathrm{\Phi }}_n(x)$为：

$${\mathrm{\Phi }}_n(x)=1+x+x^2+\dots +x^{n-1}=\sum _{k=0}^{n-1}{x}^k$$

这里的$x^{n-1}$表示最高次幂是$n-1$的项，系数$1,x,x^2,\dots ,x^{n-1}$都是整数。

2. 如果$n=2p$，其中$p$是一个奇素数，分圆多项式${\mathrm{\Phi }}_{2p}(x)$为：

$${\mathrm{\Phi }}_{2p}(x)=1-x+x^2-\dots +(-1{)}^{p-1}{x}^{p-1}=\sum _{k=0}^{p-1}(-x{)}^k$$

在这个公式中，奇数次幂的系数是负的，这是为了满足分圆多项式的定义，其中的系数必须交替正负。

For n up to 16, the cyclotomic polynomials are:：

规范嵌入（Canonical embedding）

规范嵌入（Canonical embedding）是用于编码和解码的一种技术，常用于将向量映射到多项式空间中。规范嵌入具有很好的性质，其中一个重要性质是它们是同构的（isomorphism），即向量空间与多项式空间之间存在一一映射，保持了向量和多项式之间的关系。

具体来说，规范嵌入确保了向量空间中的每个向量都对应唯一的多项式，反之亦然。这意味着，通过规范嵌入，我们可以将向量空间中的运算映射到多项式空间中，从而实现对编码和解码过程的管理和控制.

同构性质使得向量和多项式之间的转换更加灵活和高效，这在许多应用中都是非常有用的，尤其是在使用多项式表示数据时，比如在密码学中的同态加密方案中。

让我们通过一个具体的例子来进一步理解规范嵌入（Canonical embedding）的概念及其在将向量映射到多项式空间中的应用。

假设我们有一个三维向量空间${\mathbb{R}}^3$，并想要将这个空间中的向量映射到二次多项式空间${\mathbb{R}}_2[x]$（即所有形如$a{x}^2+bx+c$的多项式构成的空间）中,==一个$n-1$次多项式在$n$个不同点的取值唯一确定了该多项式==。

我们可以定义如下的规范嵌入映射：

$$\varphi :{\mathbb{R}}^3\to {\mathbb{R}}_2[x]$$$$\varphi (a,b,c)=a^{{}^{\prime }}{x}^2+b^{{}^{\prime }}x+c^{{}^{\prime }}$$

这里，向量$(a,b,c)$被直接映射到一个二次多项式$a^{{}^{\prime }}{x}^2+b^{{}^{\prime }}x+c^{{}^{\prime }}$上。此映射是线性的，并且是一个同构映射，因为它是双射（即一一对应且满射）并且保留了向量空间的线性结构。

同构的性质：

1. 一一对应：每个向量$(a,b,c)$都映射到一个唯一确定的多项式$a^{{}^{\prime }}{x}^2+b^{{}^{\prime }}x+c^{{}^{\prime }}$，反之亦然。

2. 运算保持：如果在向量空间中定义了向量的加法和标量乘法，那么这些运算通过映射$\varphi$​ 直接转换为多项式的相应运算：

   $$\varphi (a_1,b_1,c_1)+\varphi (a_2,b_2,c_2)=(a_1^{{}^{\prime }}+a_2^{{}^{\prime }})x^2+(b_1^{{}^{\prime }}+b_2^{{}^{\prime }})x+(c_1^{{}^{\prime }}+c_2^{{}^{\prime }})$$$$\lambda \varphi (a,b,c)=(\lambda a^{{}^{\prime }})x^2+(\lambda b^{{}^{\prime }})x+(\lambda c^{{}^{\prime }})$$

这种映射方式使得原始的向量空间运算可以无缝地转换成多项式空间中的运算，非常适合在计算和理论分析中使用。

在密码学中，这种类型的嵌入尤其有用，例如在设计同态加密算法时。同态加密算法允许在加密数据上直接进行某些类型的计算，而无需先解密数据。通过规范嵌入，我们可以将实际的数据向量编码为多项式，然后在多项式形式的加密数据上执行运算，最后再解码回原始数据向量，而在整个过程中数据始终保持加密状态。

Encoding in CKKS

CKKS利用整数多项式环的丰富结构来构建其明文空间和密文空间。然而，数据更常见地以向量的形式出现，而不是多项式的形式。

因此，有必要将输入$z\in {\mathbb{C}}^{N/2}$编码成一个多项式$m(X)\in \mathbb{Z}[X]/(X^N+1)$。

我们将我们的多项式的度数模数记为$N$，它将是2的幂。我们用${\mathrm{\Phi }}_M(X)=X^N+1$表示第$m$个分圆多项式（注意这里$M=2N$）。明文空间将是多项式环$R=\mathbb{Z}[X]/(X^N+1)$。让我们用${\xi }_M$表示第$M$个单位根：${\xi }_M=e^{2i\pi /M}$。

为了理解如何将向量编码为多项式以及多项式上的计算如何反映在底层向量中，我们首先通过一个简单的示例来实验，其中我们简单地将一个向量$z\in {\mathbb{C}}^N$编码为一个多项式$m(X)\in \mathbb{C}[X]/(X^N+1)$。然后，我们将讨论CKKS的实际编码，它将一个向量$z\in {\mathbb{C}}^{N/2}$编码成一个多项式$m(X)\in \mathbb{Z}[X]/(X^N+1)$。

Vanilla Encoding

在这里，我们将讨论简单情况下将$z\in {\mathbb{C}}^N$编码成多项式$m(X)\in \mathbb{C}[X]/(X^N+1)$。

为此，我们将使用规范嵌入$\sigma :\mathbb{C}[X]/(X^N+1)\to {\mathbb{C}}^N$，它解码和编码我们的向量。

这个想法很简单：要将多项式$m(X)$解码为向量$z$，我们在某些值上评估多项式，这些值将是分圆多项式${\mathrm{\Phi }}_M(X)=X^N+1$的根。这些$N$个根是：$\xi ,{\xi }^3,\dots ,{\xi }^{2N-1}$。

因此，要解码一个多项式$m(X)$，我们定义$\sigma (m)=(m(\xi ),m({\xi }^3),\dots ,m({\xi }^{2N-1}))\in {\mathbb{C}}^N$。注意，$\sigma$定义了一个同构，这意味着它是一个双射同态，因此任何向量将被唯一编码为其相应的多项式，反之亦然。

==棘手的部分是将一个向量$z\in {\mathbb{C}}^N$编码成相应的多项式，这意味着计算逆变换${\sigma }^{-1}$==。因此，==问题就是找到一个多项式==$m(X)=\sum _{i=0}^{N-1}{\alpha }_i{X}^i\in \mathbb{C}[X]/(X^N+1)$，给定一个向量$z\in {\mathbb{C}}^N$，使得$\sigma (m)=(m(\xi ),m({\xi }^3),\dots ,m({\xi }^{2N-1}))=(z_1,\dots ,z_N)$。

进一步追求这个线索，我们得到以下方程组：

$$\sum _{j=0}^{N-1}{\alpha }_j({\xi }^{2i-1}{)}^j=z_i,i=1,\dots ,N.$$

这可以看作矩阵相乘：

$$\left[\begin{array}{ccccc}1& {\xi }^1& {\xi }^2& \cdots & {\xi }^{N-1}\\ 1& ({\xi }^3{)}^1& ({\xi }^3{)}^2& \cdots & ({\xi }^3{)}^{N-1}\\ 1& ({\xi }^5{)}^1& ({\xi }^5{)}^2& \cdots & ({\xi }^5{)}^{N-1}\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ 1& ({\xi }^{2N-1}{)}^1& ({\xi }^{2N-1}{)}^2& \cdots & ({\xi }^{2N-1}{)}^{N-1}\end{array}\right]\left[\begin{array}{c}{a}_0\\ a_1\\ a_2\\ ⋮\\ a_{N-1}\end{array}\right]=\left[\begin{array}{c}{z}_1\\ z_2\\ z_3\\ ⋮\\ z_N\end{array}\right]$$

---

$$A\alpha =z$$

其中$A$是$N$个根$({\xi }^{2i-1}{)}_{i=1,\dots ,N}$的范德蒙德矩阵，$\alpha$是多项式系数的向量，$z$是我们想要编码的向量。

因此我们有：$\alpha =A^{-1}z$，并且${\sigma }^{-1}(z)=\sum _{i=0}^{N-1}{\alpha }_i{X}^i\in \mathbb{C}[X]/(X^N+1)$。

Example

让我们现在看一个例子，以更好地理解我们到目前为止所讨论的内容。

设$M=8$，$N=M/2=4$，${\mathrm{\Phi }}_M(X)=X^4+1$，$\omega =e^{2i\pi /8}=e^{i\pi /4}$。
我们的目标是编码以下向量：$[1,2,3,4]$和$[-1,-2,-3,-4]$，对它们进行解码，然后对它们的多项式进行加法和乘法，并最终解码结果。

正如我们所看到的，在解码多项式时，我们只需要在M次单位根的幂上对其进行评估。在这里，我们选择${\xi }_M=\omega =e^{i\pi /4}$。

一旦我们有了$\xi$和$M$，我们就可以定义$\sigma$及其逆${\sigma }^{-1}$，分别用于解码和编码。