CKKS EXPLAINED, PART 5: RESCALING

Introduction

在之前的 CKKS 解释系列文章的第四部分《乘法和重线性化》中，我们了解了 CKKS 中的密文乘法是如何工作的，为什么我们需要对输出进行重线性化以保持密文大小不变，以及如何执行重线性化操作。

然而，正如我们将要看到的，我们还需要进行一种称为重新缩放的最终操作，以管理噪声并避免溢出。这将是本系列的最后一个理论文章，在下一篇也是最后一篇文章中，我们将使用 Python 实现所有内容！

为了理解这个过程是如何工作的，首先1我们将从高层次的角度来看，然后再深入了解其详细工作原理。

High level view of the modulus chain

到目前为止，我们已经深入研究了CKKS的细节，但是在这里我们将退后一步。CKKS使用所谓的级别（levels）进行工作，这意味着在噪声增加到无法正确解密输出之前，只允许进行有限次数的乘法操作。

您可以将其想象为一个汽车油箱。最初，油箱是满的，但随着进行越来越多的操作，油箱会逐渐耗尽，直到没有油了，您将无法再进行任何操作。同样，级别化同态加密方案也是如此：您首先具有一定数量的“油”，但是随着进行乘法操作，您的“油”会越来越少，直到耗尽，您将无法执行任何操作。

下图说明了这一点。当您开始时，您拥有初始的满油箱。但随着进行乘法和重新缩放操作，您将失去级别（level），这相当于消耗了一部分“油”。因此，如果您从L个级别开始，表示为$q_L,q_{L-1},\dots ,q_1$，处于级别$q_l$意味着您还剩下$l$次乘法操作，执行一次乘法将级别从$q_l$降低到$q_{l-1}$。

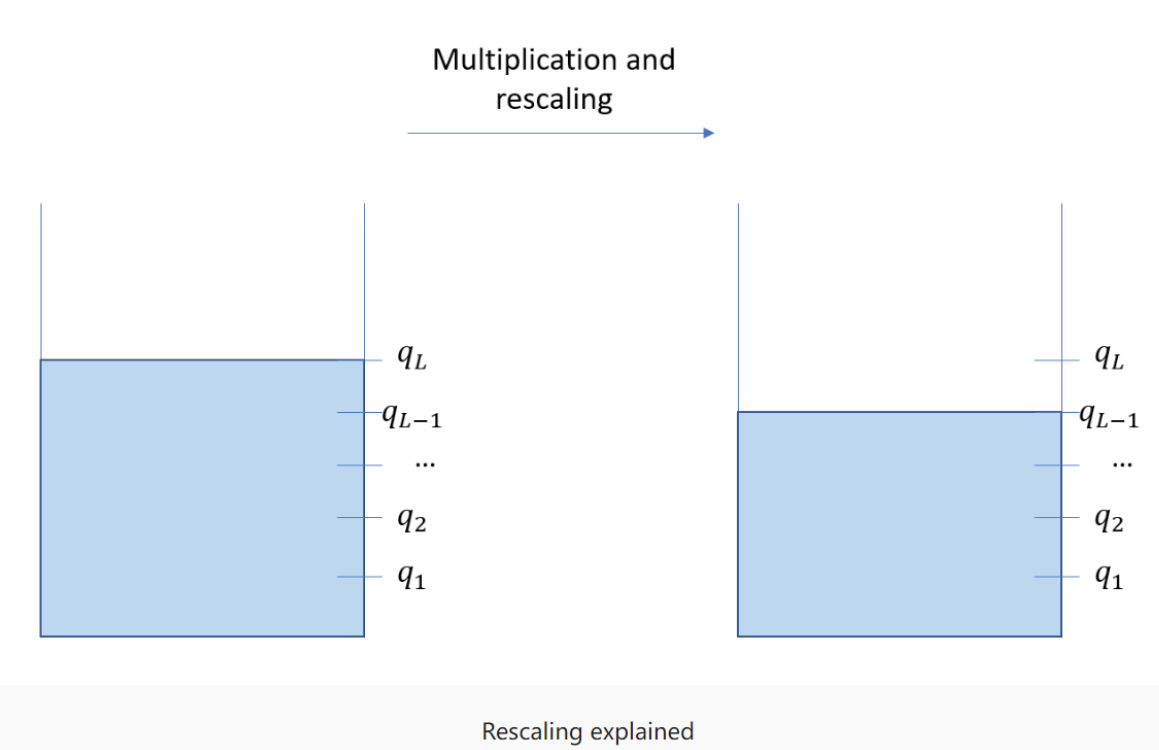
当您的“汽油”耗尽时，在现实生活中您可以加油以便继续前行。这个操作被称为自举（bootstrapping），我们在本文中不会涉及到。因此，如果我们假设没有机会给油箱加油，使用级别化同态加密方案时需要考虑一个有趣的方面：==您需要预先知道要执行的乘法次数！==

事实上，就像在现实生活中一样，如果您计划前往较远的地方，您需要的汽油数量会比您只在附近行驶时多。在这里也是如此，根据您需要执行的乘法次数的多少，您需要调整油箱的大小。但是油箱越大，计算的负担就越重，参数的安全性也越低。事实上，就像在现实生活中一样，如果您需要更大的油箱，它会更重，使事情变慢，并且会降低安全性。

我们不会详细介绍所有细节，但是需要知道 CKKS 方案的难度是基于比率$\frac{N}{q}$，其中$N$是我们多项式的次数，即我们向量的大小，$q$是系数模数，即我们的油箱大小。

因此，我们需要的乘法次数越多，油箱越大，因此我们的参数变得不那么安全。为了保持相同的安全级别，我们需要增加$N$，这将增加我们操作的计算成本。

下图来自 Microsoft Private AI Bootcamp，显示了在使用 CKKS 时必须考虑的权衡。为了保证 128 位的安全性，我们必须增加多项式的次数，即使我们不需要额外的插槽，因为模增加可能会使我们的参数不安全。

在我们继续更深入的理论部分之前，让我们总结一下关键要点：

• 重新缩放和噪声管理可以看作是管理一个汽车油箱，您从一个初始预算开始，随着使用次数的增加而逐渐减少。如果油耗尽，您将无法再继续操作。
• 您需要事先知道要执行多少次乘法，这将决定油箱的大小，并影响您将使用的多项式次数的大小。

Context

现在我们来看一下更详细的原因和工作原理。

如果您还记得第二部分关于编码的内容，如果我们有一个初始的数值向量$z$，在编码过程中会乘以一个尺度$\mathrm{\Delta }$来保持一定的精度。

因此，明文$\mu$和密文$c$中包含的基本值是$\mathrm{\Delta }\cdot z$。当我们将两个密文$c$和$c^{\prime }$相乘时，结果中包含了$z\cdot z^{\prime }\cdot {\mathrm{\Delta }}^2$。因此，它包含了尺度的平方，这可能导致在几次乘法后发生溢出，因为尺度可能呈指数级增长。此外，正如我们之前所看到的，每次乘法后噪声都会增加。

因此，重新缩放操作的目的实际上是保持尺度恒定，并减少密文中存在的噪声。

Vanilla solution

那么我们如何解决这个问题呢？为此，我们需要看一下如何定义$q$。请记住，参数$q$被用作多项式环$R_q={\mathbb{Z}}_q[X]/(X^N+1)$中系数的模数。

如高层次视图所述，$q$将被用作一个我们会逐步耗尽的“油箱”，用于我们的操作。

假设我们需要执行$L$次乘法，使用尺度$\mathrm{\Delta }$，那么我们将定义$q$如下：

$$q={\mathrm{\Delta }}^L\cdot q_0$$

其中$q_0\ge \mathrm{\Delta }$，它将决定我们希望在小数部分之前有多少位。实际上，如果我们假设我们希望小数部分具有 30 位的精度，并且整数部分具有 10 位的精度，我们将设置：

$$\mathrm{\Delta }=2^{30}，q_0=2^{\text{bits integer}}\cdot 2^{\text{bits decimal}}=2^{10+30}=2^{40}。$$

一旦我们确定了整数部分和小数部分的精度要求，选择了要执行的乘法次数$L$，并相应地设置了$q$，定义重新缩放操作就非常简单了：我们只需对密文进行除法和四舍五入即可。

确实，假设我们在给定的级别$l$上，模数为$q_l$。我们有一个密文$c\in {\mathcal{R}}_{{\mathcal{q}}_{\mathcal{l}}}^{\mathcal{2}}$。然后我们可以定义从级别$l$到$l-1$的重新缩放操作为：

$$R{S}_{l\to l-1}(c)=\lfloor \frac{q_{l-1}}{q_l}\cdot c\rceil mod{q}_{l-1}=\lfloor {\mathrm{\Delta }}^{-1}\cdot c\rceil mod{q}_{l-1}，$$

其中$q_l={\mathrm{\Delta }}^l\cdot q_0$。

通过这样做，我们成功做到了两件事：

1. 在解密两个密文$c,c^{\prime }$的乘积后，底层值为$\mathrm{\Delta }\cdot z,\mathrm{\Delta }\cdot z^{\prime }$，应用重新缩放后，我们得到了$\mathrm{\Delta }\cdot z\cdot z^{\prime }$。因此，只要我们在每次乘法后进行重新缩放，尺度就会保持恒定。
2. 噪声被减少，因为我们不仅除以底层明文值，还除以解密的噪声部分，记为$\mu +e$。因此，重新缩放也用于噪声的减少。

因此，将所有内容综合起来，在CKKS中执行乘法需要完成三件事：

1. 计算乘积：$c_{mult}=CMult(c,c^{\prime })=(d_0,d_1,d_2)$。
2. 进行线性化：$c_{relin}=Relin((d_0,d_1,d_2),evk)$。
3. 进行重新缩放：$c_{rs}=R{S}_{l\to l-1}(c)$。

完成所有这些步骤后，使用秘密密钥进行解密将提供正确的结果，我们就完成了！嗯，几乎完成了，因为还有最后一个细节需要讨论。

Chinese remainder theorem

我们已经看到我们拥有了所需的一切，但是有一个技术问题：计算是在巨大的数字上进行的！实际上，我们的操作是在巨大的模数$ql={\mathrm{\Delta }}^l\cdot q_0$下进行的。例如，假设我们希望小数部分有30位精度，整数部分有10位精度，并且进行10次乘法。那么我们有$q_L={\mathrm{\Delta }}^L\cdot q_0=2^{30\cdot 10+40}=2^{340}$！

因为我们有时会处理巨大的多项式，比如均匀采样的多项式，一些计算无法适应常规的64位系统，因此我们必须找到一种解决方法。

这就是中国剩余定理的用武之地！该定理指出，如果我们有$L$个互质的数$p_1,\dots ,p_L$，$p=\prod _{l=1}^L{p}_l$是它们的乘积，那么映射

$$\mathbb{Z}/p\mathbb{Z}\to \mathbb{Z}/p_1\mathbb{Z}\times \cdots \times \mathbb{Z}/p_L\mathbb{Z}:x(\mathrm{mod}p)\mapsto (x(\mathrm{mod}{p}_1),\dots ,x(\mathrm{mod}{p}_L))$$

是一个环同构，也就是说，如果您想在“大”的环$\mathbb{Z}/p\mathbb{Z}$上进行算术运算，您可以在“小”的环$\mathbb{Z}/p_l\mathbb{Z}$上独立进行，这样就不会遇到超过64位的计算问题。

因此，在实践中，我们首先选择$p_1,\dots ,p_L,q_0$是素数，其中每个$p_l\approx \mathrm{\Delta }$，$q_0$是一个大于$\mathrm{\Delta }$的素数，取决于所需的整数精度，然后设置$q_L=\prod _{l=1}^L{p}_l\cdot q_0$。

这样，我们可以使用中国剩余定理，并通过上面描述的小技巧来进行具有大模数的算术运算。重新缩放操作必须稍作修改：

$$R{S}_{l\to l-1}(c)=\lfloor \frac{q_{l-1}}{q_l}c\rceil (\mathrm{mod}{q}_{l-1})=\lfloor p_l^{-1}c\rceil (\mathrm{mod}{q}_{l-1})。$$

因此，在本文中，我们已经了解了重新缩放是什么，为什么我们需要它，以及如何在实践中实现它。在下一篇也是最后一篇文章中，我们将把所有内容整合起来，在Python中编写一个类似CKKS的同态加密方案！