DES加密算法详解

# DES加密算法详解

提示

当涉及数据加密时，DES（Data Encryption Standard）算法是一种经典且常用的对称密钥加密算法。DES算法被广泛应用于保护敏感数据，比如银行交易和网络通信。虽然现在已经被更强大的加密算法所取代，但了解DES的基本原理仍然具有重要意义。本文将介绍DES算法的工作原理，以及使用简单的示例和图表来说明其过程。

# 什么是DES算法？

DES 是一种分组密码，采用64位的数据块和56位的密钥，并通过一系列复杂的置换、替换和轮函数来加密数据。它的核心思想是将输入数据进行多轮加密和混淆，最终得到输出密文。

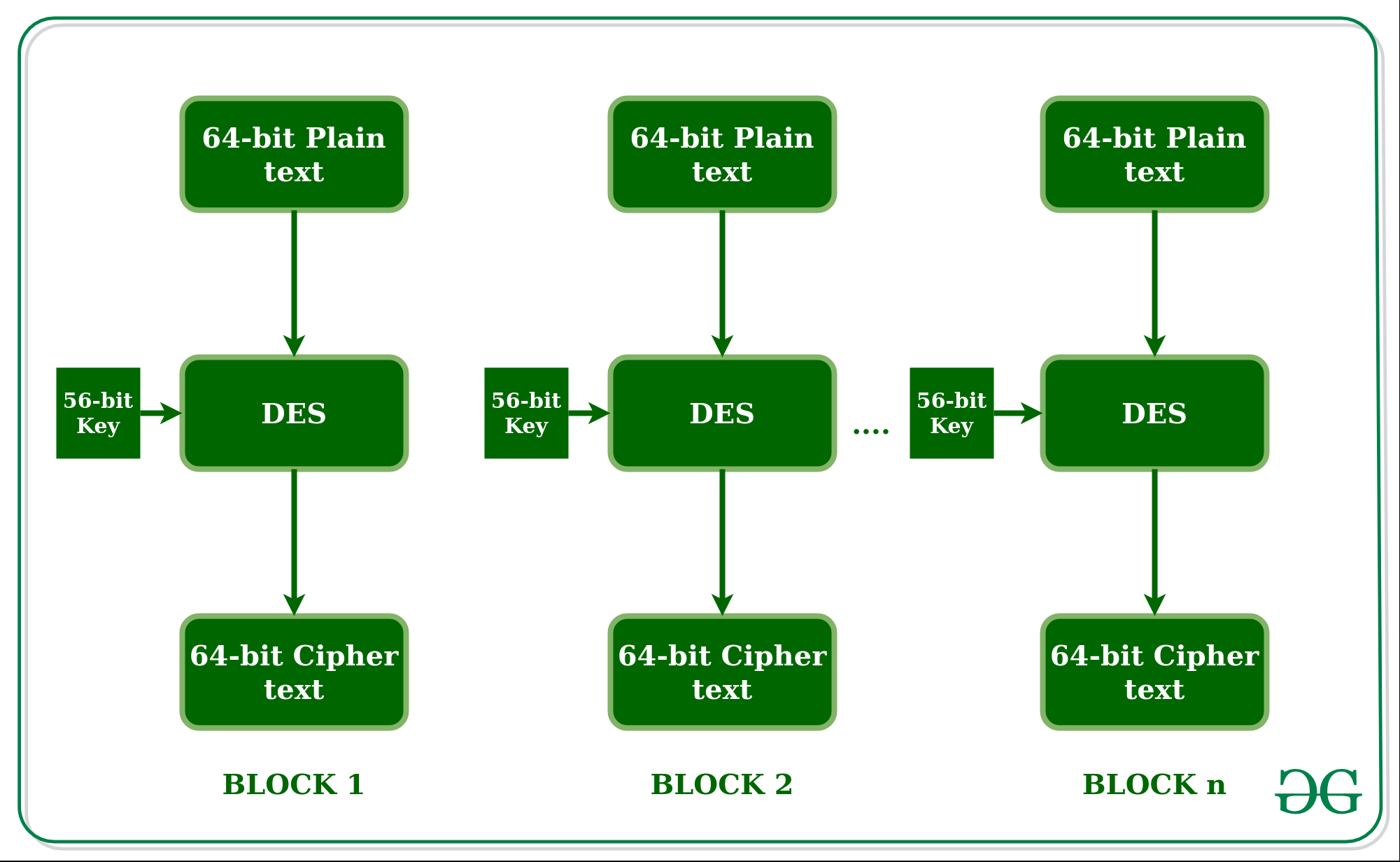
密钥长度64位，事实上是56位参与DES运算（第8、16、24、32、40、48、56、64位是校验位，使得每个密钥都有奇数个1），分组后的明文组和56位的密钥按位替代或交换的方式形成密文组。

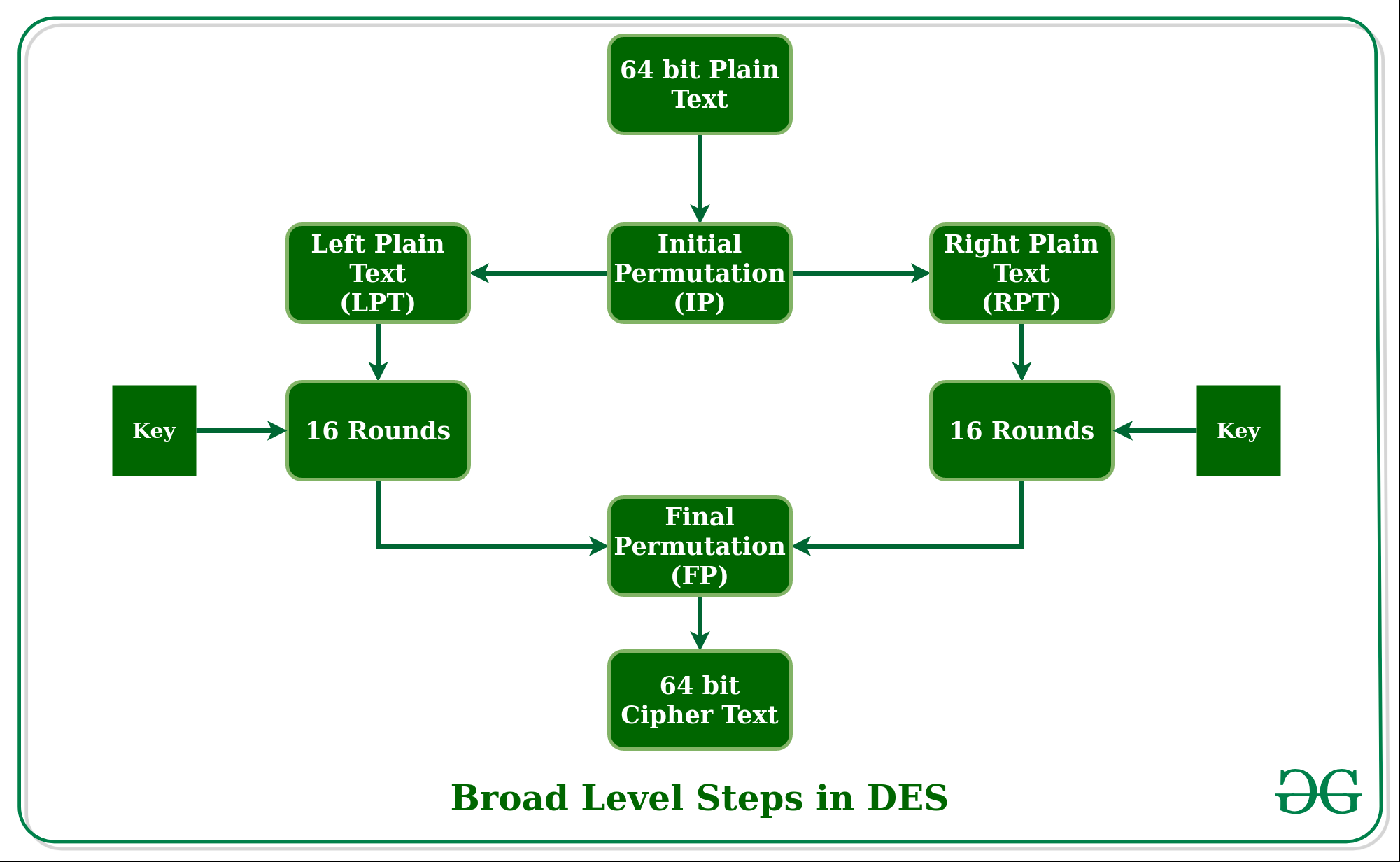
# DES算法步骤

流程图如下：

# 1.初始置换（IP置换）

初始置换（Initial Permutation）是DES算法中的第一步，它是对输入的64位明文数据进行重排的过程。初始置换的目的是将输入的数据按照一定规则重新排列，以便更好地适应后续的加密处理。

初始置换使用一个固定的置换表（Permutation Table）来对输入的64位明文进行重排。该表定义了明文数据从输入到输出的映射关系。在初始置换过程中，输入的每一位数据都会被放置在一个新的位置上，形成一个新的64位数据块。

置换规则如下表所示：

58 60 62 64 57 59 61 63
50 52 54 56 49 51 53 55
42 44 46 48 41 43 45 47
34 36 38 40 33 35 37 39
26 28 30 32 25 27 29 31
18 20 22 24 17 19 21 23
10 12 14 16  9 11 13 15
2   4  6  8  1  3  5  7

1
2
3
4
5
6
7
8
9
10

具体的置换过程如下：

输入的第58位数据将成为新数据的第1位。
输入的第60位数据将成为新数据的第2位。
输入的第62位数据将成为新数据的第3位。
输入的第64位数据将成为新数据的第4位。
输入的第57位数据将成为新数据的第5位。
依次类推...

经过这个置换过程后，原始的64位明文数据将被重新排列成一个新的64位数据块，置换后的数据分为L0和R0两部分，L0为新数据的左32位，R0为新数据的右32位。DES算法的加密过程涉及16轮迭代，每轮迭代都会对L0和R0进行处理。

# 2. 子秘钥生成

子密钥生成是DES算法的一个重要步骤，它负责生成16轮加密过程中所需的子密钥。DES算法使用一个64位的初始密钥（K），经过初始密钥置换（PC-1）得到一个56位的密钥（C0和D0）。然后，根据每一轮所需的位移数（shifts）和压缩置换表（PC-2），生成16组48位的子密钥（K1到K16）。

下面是子密钥生成的详细步骤：

初始密钥置换（PC-1）：

初始密钥（K）：1010000010101010100010101100101001000110111101011100100110110011

初始置换表（PC-1）：

58 50 42 34 26 18 10 2
60 52 44 36 28 20 12 4
62 54 46 38 30 22 14 6
64 56 48 40 32 24 16 8
57 49 41 33 25 17 9 1
59 51 43 35 27 19 11 3
61 53 45 37 29 21 13 5
63 55 47 39 31 23 15 7

1
2
3
4
5
6
7
8

将初始密钥按照置换表进行重排，得到56位的C0和D0，C0和D0分别代表了初始密钥的左半部分和右半部分。：

C0：111000000000111000000110011100001110010001110010
D0：000110000001001000011100001010001001101001000010

1
2

子密钥位移（Shifts）：

根据DES算法规定的位移数表（Shift Table），对C0和D0进行循环左移。每一轮左移的位数由位移数表给出：

1 1 2 2 2 2 2 2 1 2 2 2 2 2 2 1

按照位移数表，对C0和D0进行左移操作，得到C1和D1：

C1：110000000001110000001100111000011100100011100100
D1：001100000010010000111000010100010011010010000101

1
2

压缩置换（PC-2）：

将C1和D1合并成56位的数据，并按照压缩置换表（PC-2）进行重排，得到48位的子密钥K1：

压缩置换表（PC-2）：

14 17 11 24 1 5 3 28
15 6 21 10 23 19 12 4
26 8 16 7 27 20 13 2
41 52 31 37 47 55 30 40
51 45 33 48 44 49 39 56
34 53 46 42 50 36 29 32

1
2
3
4
5
6

子密钥K1：110001000110101011001001011010111100001011010010

重复循环：

重复上述步骤16次，每一轮得到一个新的子密钥Ki（i从1到16），用于后续16轮的加密过程。

# 3.16轮迭代加密

接下来是DES算法的第二步，即16轮迭代。在这个步骤中，DES算法使用子密钥Ki（i从1到16）对数据进行加密。每一轮迭代使用一个不同的子密钥Ki，从而对数据进行混淆和置换，增加加密的强度和随机性。

每一轮迭代的过程如下：

将输入的64位数据块分为左半部分L和右半部分R，各32位。
将R作为轮函数（Feistel Function）的输入，与当前轮的子密钥Ki进行异或运算。
将异或运算的结果作为轮函数的输入，经过扩展置换（E-Expansion），将32位数据扩展为48位。
将扩展后的48位数据与子密钥Ki进行异或运算。
将异或运算的结果分为8组，每组6位。每组6位数据作为S盒（Substitution Box）的输入，经过S盒代换得到4位输出。
将S盒代换的结果进行P置换（Permutation），将每组4位数据重新排列，得到32位输出。
将P置换的结果与左半部分L进行异或运算，得到新的右半部分R。
将原始的右半部分R作为新的左半部分L。
重复以上步骤进行16轮迭代。

每一轮迭代的关键是轮函数（Feistel Function），它对32位数据进行扩展、异或运算、S盒代换和P置换，从而将每一轮的输入数据混淆和置换，增加DES算法的复杂性和安全性。

最后一轮迭代完成后，左半部分L和右半部分R进行交换，得到新的64位数据块。经过16轮迭代后，得到的64位数据块称为加密的密文（Ciphertext）。该密文与初始置换的过程相反，进行逆初始置换也称FP（Inverse Initial Permutation，IP^(-1)），得到最终的64位加密密文。

# 3. 逆初始置换（FP）

逆初始置换是DES算法的倒数第二步，它是对经过16轮迭代后得到的64位数据块进行重排的过程。逆初始置换使用一个固定的置换表，与初始置换相对应，将64位数据按照一定规则重新排列，得到一个新的64位数据块。

逆初始置换的过程与初始置换相反，它将经过16轮迭代后得到的数据块中的每一位数据，按照置换表的规则重新排列，形成一个新的64位数据块。

逆初始置换保证了最终的密文数据与初始明文数据有一定的关联，同时消除了加密过程中的置换操作带来的影响，从而得到最终的加密结果。

# 4. 生成密文（Ciphertext）

经过逆初始置换后，得到的64位数据块就是最终的密文（Ciphertext）。该密文是经过DES算法加密后的结果，具有很高的安全性和随机性。

最终的密文可以发送给接收方，接收方使用相同的密钥和DES算法的解密过程，对密文进行解密，恢复成原始的明文数据。

代码：

# Python3 code for the above approach

# Hexadecimal to binary conversion
def hex2bin(s):
	mp = {'0': "0000",
		'1': "0001",
		'2': "0010",
		'3': "0011",
		'4': "0100",
		'5': "0101",
		'6': "0110",
		'7': "0111",
		'8': "1000",
		'9': "1001",
		'A': "1010",
		'B': "1011",
		'C': "1100",
		'D': "1101",
		'E': "1110",
		'F': "1111"}
	bin = ""
	for i in range(len(s)):
		bin = bin + mp[s[i]]
	return bin

# Binary to hexadecimal conversion


def bin2hex(s):
	mp = {"0000": '0',
		"0001": '1',
		"0010": '2',
		"0011": '3',
		"0100": '4',
		"0101": '5',
		"0110": '6',
		"0111": '7',
		"1000": '8',
		"1001": '9',
		"1010": 'A',
		"1011": 'B',
		"1100": 'C',
		"1101": 'D',
		"1110": 'E',
		"1111": 'F'}
	hex = ""
	for i in range(0, len(s), 4):
		ch = ""
		ch = ch + s[i]
		ch = ch + s[i + 1]
		ch = ch + s[i + 2]
		ch = ch + s[i + 3]
		hex = hex + mp[ch]

	return hex

# Binary to decimal conversion


def bin2dec(binary):

	binary1 = binary
	decimal, i, n = 0, 0, 0
	while(binary != 0):
		dec = binary % 10
		decimal = decimal + dec * pow(2, i)
		binary = binary//10
		i += 1
	return decimal

# Decimal to binary conversion


def dec2bin(num):
	res = bin(num).replace("0b", "")
	if(len(res) % 4 != 0):
		div = len(res) / 4
		div = int(div)
		counter = (4 * (div + 1)) - len(res)
		for i in range(0, counter):
			res = '0' + res
	return res

# Permute function to rearrange the bits


def permute(k, arr, n):
	permutation = ""
	for i in range(0, n):
		permutation = permutation + k[arr[i] - 1]
	return permutation

# shifting the bits towards left by nth shifts


def shift_left(k, nth_shifts):
	s = ""
	for i in range(nth_shifts):
		for j in range(1, len(k)):
			s = s + k[j]
		s = s + k[0]
		k = s
		s = ""
	return k

# calculating xow of two strings of binary number a and b


def xor(a, b):
	ans = ""
	for i in range(len(a)):
		if a[i] == b[i]:
			ans = ans + "0"
		else:
			ans = ans + "1"
	return ans


# Table of Position of 64 bits at initial level: Initial Permutation Table
initial_perm = [58, 50, 42, 34, 26, 18, 10, 2,
				60, 52, 44, 36, 28, 20, 12, 4,
				62, 54, 46, 38, 30, 22, 14, 6,
				64, 56, 48, 40, 32, 24, 16, 8,
				57, 49, 41, 33, 25, 17, 9, 1,
				59, 51, 43, 35, 27, 19, 11, 3,
				61, 53, 45, 37, 29, 21, 13, 5,
				63, 55, 47, 39, 31, 23, 15, 7]

# Expansion D-box Table
exp_d = [32, 1, 2, 3, 4, 5, 4, 5,
		6, 7, 8, 9, 8, 9, 10, 11,
		12, 13, 12, 13, 14, 15, 16, 17,
		16, 17, 18, 19, 20, 21, 20, 21,
		22, 23, 24, 25, 24, 25, 26, 27,
		28, 29, 28, 29, 30, 31, 32, 1]

# Straight Permutation Table
per = [16, 7, 20, 21,
	29, 12, 28, 17,
	1, 15, 23, 26,
	5, 18, 31, 10,
	2, 8, 24, 14,
	32, 27, 3, 9,
	19, 13, 30, 6,
	22, 11, 4, 25]

# S-box Table
sbox = [[[14, 4, 13, 1, 2, 15, 11, 8, 3, 10, 6, 12, 5, 9, 0, 7],
		[0, 15, 7, 4, 14, 2, 13, 1, 10, 6, 12, 11, 9, 5, 3, 8],
		[4, 1, 14, 8, 13, 6, 2, 11, 15, 12, 9, 7, 3, 10, 5, 0],
		[15, 12, 8, 2, 4, 9, 1, 7, 5, 11, 3, 14, 10, 0, 6, 13]],

		[[15, 1, 8, 14, 6, 11, 3, 4, 9, 7, 2, 13, 12, 0, 5, 10],
		[3, 13, 4, 7, 15, 2, 8, 14, 12, 0, 1, 10, 6, 9, 11, 5],
		[0, 14, 7, 11, 10, 4, 13, 1, 5, 8, 12, 6, 9, 3, 2, 15],
		[13, 8, 10, 1, 3, 15, 4, 2, 11, 6, 7, 12, 0, 5, 14, 9]],

		[[10, 0, 9, 14, 6, 3, 15, 5, 1, 13, 12, 7, 11, 4, 2, 8],
		[13, 7, 0, 9, 3, 4, 6, 10, 2, 8, 5, 14, 12, 11, 15, 1],
		[13, 6, 4, 9, 8, 15, 3, 0, 11, 1, 2, 12, 5, 10, 14, 7],
		[1, 10, 13, 0, 6, 9, 8, 7, 4, 15, 14, 3, 11, 5, 2, 12]],

		[[7, 13, 14, 3, 0, 6, 9, 10, 1, 2, 8, 5, 11, 12, 4, 15],
		[13, 8, 11, 5, 6, 15, 0, 3, 4, 7, 2, 12, 1, 10, 14, 9],
		[10, 6, 9, 0, 12, 11, 7, 13, 15, 1, 3, 14, 5, 2, 8, 4],
		[3, 15, 0, 6, 10, 1, 13, 8, 9, 4, 5, 11, 12, 7, 2, 14]],

		[[2, 12, 4, 1, 7, 10, 11, 6, 8, 5, 3, 15, 13, 0, 14, 9],
		[14, 11, 2, 12, 4, 7, 13, 1, 5, 0, 15, 10, 3, 9, 8, 6],
		[4, 2, 1, 11, 10, 13, 7, 8, 15, 9, 12, 5, 6, 3, 0, 14],
		[11, 8, 12, 7, 1, 14, 2, 13, 6, 15, 0, 9, 10, 4, 5, 3]],

		[[12, 1, 10, 15, 9, 2, 6, 8, 0, 13, 3, 4, 14, 7, 5, 11],
		[10, 15, 4, 2, 7, 12, 9, 5, 6, 1, 13, 14, 0, 11, 3, 8],
		[9, 14, 15, 5, 2, 8, 12, 3, 7, 0, 4, 10, 1, 13, 11, 6],
		[4, 3, 2, 12, 9, 5, 15, 10, 11, 14, 1, 7, 6, 0, 8, 13]],

		[[4, 11, 2, 14, 15, 0, 8, 13, 3, 12, 9, 7, 5, 10, 6, 1],
		[13, 0, 11, 7, 4, 9, 1, 10, 14, 3, 5, 12, 2, 15, 8, 6],
		[1, 4, 11, 13, 12, 3, 7, 14, 10, 15, 6, 8, 0, 5, 9, 2],
		[6, 11, 13, 8, 1, 4, 10, 7, 9, 5, 0, 15, 14, 2, 3, 12]],

		[[13, 2, 8, 4, 6, 15, 11, 1, 10, 9, 3, 14, 5, 0, 12, 7],
		[1, 15, 13, 8, 10, 3, 7, 4, 12, 5, 6, 11, 0, 14, 9, 2],
		[7, 11, 4, 1, 9, 12, 14, 2, 0, 6, 10, 13, 15, 3, 5, 8],
		[2, 1, 14, 7, 4, 10, 8, 13, 15, 12, 9, 0, 3, 5, 6, 11]]]

# Final Permutation Table
final_perm = [40, 8, 48, 16, 56, 24, 64, 32,
			39, 7, 47, 15, 55, 23, 63, 31,
			38, 6, 46, 14, 54, 22, 62, 30,
			37, 5, 45, 13, 53, 21, 61, 29,
			36, 4, 44, 12, 52, 20, 60, 28,
			35, 3, 43, 11, 51, 19, 59, 27,
			34, 2, 42, 10, 50, 18, 58, 26,
			33, 1, 41, 9, 49, 17, 57, 25]


def encrypt(pt, rkb, rk):
	pt = hex2bin(pt)

	# Initial Permutation
	pt = permute(pt, initial_perm, 64)
	print("After initial permutation", bin2hex(pt))

	# Splitting
	left = pt[0:32]
	right = pt[32:64]
	for i in range(0, 16):
		# Expansion D-box: Expanding the 32 bits data into 48 bits
		right_expanded = permute(right, exp_d, 48)

		# XOR RoundKey[i] and right_expanded
		xor_x = xor(right_expanded, rkb[i])

		# S-boxex: substituting the value from s-box table by calculating row and column
		sbox_str = ""
		for j in range(0, 8):
			row = bin2dec(int(xor_x[j * 6] + xor_x[j * 6 + 5]))
			col = bin2dec(
				int(xor_x[j * 6 + 1] + xor_x[j * 6 + 2] + xor_x[j * 6 + 3] + xor_x[j * 6 + 4]))
			val = sbox[j][row][col]
			sbox_str = sbox_str + dec2bin(val)

		# Straight D-box: After substituting rearranging the bits
		sbox_str = permute(sbox_str, per, 32)

		# XOR left and sbox_str
		result = xor(left, sbox_str)
		left = result

		# Swapper
		if(i != 15):
			left, right = right, left
		print("Round ", i + 1, " ", bin2hex(left),
			" ", bin2hex(right), " ", rk[i])

	# Combination
	combine = left + right

	# Final permutation: final rearranging of bits to get cipher text
	cipher_text = permute(combine, final_perm, 64)
	return cipher_text


pt = "123456ABCD132536"
key = "AABB09182736CCDD"

# Key generation
# --hex to binary
key = hex2bin(key)

# --parity bit drop table
keyp = [57, 49, 41, 33, 25, 17, 9,
		1, 58, 50, 42, 34, 26, 18,
		10, 2, 59, 51, 43, 35, 27,
		19, 11, 3, 60, 52, 44, 36,
		63, 55, 47, 39, 31, 23, 15,
		7, 62, 54, 46, 38, 30, 22,
		14, 6, 61, 53, 45, 37, 29,
		21, 13, 5, 28, 20, 12, 4]

# getting 56 bit key from 64 bit using the parity bits
key = permute(key, keyp, 56)

# Number of bit shifts
shift_table = [1, 1, 2, 2,
			2, 2, 2, 2,
			1, 2, 2, 2,
			2, 2, 2, 1]

# Key- Compression Table : Compression of key from 56 bits to 48 bits
key_comp = [14, 17, 11, 24, 1, 5,
			3, 28, 15, 6, 21, 10,
			23, 19, 12, 4, 26, 8,
			16, 7, 27, 20, 13, 2,
			41, 52, 31, 37, 47, 55,
			30, 40, 51, 45, 33, 48,
			44, 49, 39, 56, 34, 53,
			46, 42, 50, 36, 29, 32]

# Splitting
left = key[0:28] # rkb for RoundKeys in binary
right = key[28:56] # rk for RoundKeys in hexadecimal

rkb = []
rk = []
for i in range(0, 16):
	# Shifting the bits by nth shifts by checking from shift table
	left = shift_left(left, shift_table[i])
	right = shift_left(right, shift_table[i])

	# Combination of left and right string
	combine_str = left + right

	# Compression of key from 56 to 48 bits
	round_key = permute(combine_str, key_comp, 48)

	rkb.append(round_key)
	rk.append(bin2hex(round_key))

print("Encryption")
cipher_text = bin2hex(encrypt(pt, rkb, rk))
print("Cipher Text : ", cipher_text)

print("Decryption")
rkb_rev = rkb[::-1]
rk_rev = rk[::-1]
text = bin2hex(encrypt(cipher_text, rkb_rev, rk_rev))
print("Plain Text : ", text)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312

输出：

Encryption
After initial permutation 14A7D67818CA18AD
Round  1   18CA18AD   5A78E394   194CD072DE8C
Round  2   5A78E394   4A1210F6   4568581ABCCE
Round  3   4A1210F6   B8089591   06EDA4ACF5B5
Round  4   B8089591   236779C2   DA2D032B6EE3
Round  5   236779C2   A15A4B87   69A629FEC913
Round  6   A15A4B87   2E8F9C65   C1948E87475E
Round  7   2E8F9C65   A9FC20A3   708AD2DDB3C0
Round  8   A9FC20A3   308BEE97   34F822F0C66D
Round  9   308BEE97   10AF9D37   84BB4473DCCC
Round  10   10AF9D37   6CA6CB20   02765708B5BF
Round  11   6CA6CB20   FF3C485F   6D5560AF7CA5
Round  12   FF3C485F   22A5963B   C2C1E96A4BF3
Round  13   22A5963B   387CCDAA   99C31397C91F
Round  14   387CCDAA   BD2DD2AB   251B8BC717D0
Round  15   BD2DD2AB   CF26B472   3330C5D9A36D
Round  16   19BA9212   CF26B472   181C5D75C66D
Cipher Text :  C0B7A8D05F3A829C
Decryption
After initial permutation 19BA9212CF26B472
Round  1   CF26B472   BD2DD2AB   181C5D75C66D
Round  2   BD2DD2AB   387CCDAA   3330C5D9A36D
Round  3   387CCDAA   22A5963B   251B8BC717D0
Round  4   22A5963B   FF3C485F   99C31397C91F
Round  5   FF3C485F   6CA6CB20   C2C1E96A4BF3
Round  6   6CA6CB20   10AF9D37   6D5560AF7CA5
Round  7   10AF9D37   308BEE97   02765708B5BF
Round  8   308BEE97   A9FC20A3   84BB4473DCCC
Round  9   A9FC20A3   2E8F9C65   34F822F0C66D
Round  10   2E8F9C65   A15A4B87   708AD2DDB3C0
Round  11   A15A4B87   236779C2   C1948E87475E
Round  12   236779C2   B8089591   69A629FEC913
Round  13   B8089591   4A1210F6   DA2D032B6EE3
Round  14   4A1210F6   5A78E394   06EDA4ACF5B5
Round  15   5A78E394   18CA18AD   4568581ABCCE
Round  16   14A7D678   18CA18AD   194CD072DE8C
Plain Text :  123456ABCD132536

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

# 总结

综上所述，DES算法是一种对称密钥加密算法，它使用相同的密钥进行加密和解密。DES算法的步骤包括初始置换、16轮迭代、逆初始置换和生成密文。在16轮迭代中，使用不同的子密钥对数据进行混淆和置换，增加了算法的复杂性和安全性。
DES算法在过去曾经是使用最广泛的加密算法之一，但随着计算机技术的发展，DES的密钥长度过短，容易受到暴力破解攻击。因此，目前已经不再推荐使用DES算法来保护重要数据的安全。取而代之的是使用更安全的加密算法，如AES（Advanced Encryption Standard）。AES使用128位、192位或256位密钥长度，提供更高的安全性和保密性，是当前广泛使用的对称密钥加密算法。

编辑

上次更新: 2025/04/01, 01:48:12

← Chapter 11:Key Management and the Public-Key Revolution RSA乘法同态→