使用K-Means算法进行数据聚类：以鸢尾花数据集为例

K-Means聚类算法是机器学习中一个强大的工具，用于将数据点分组成不同的簇。本文将介绍如何使用Python中的Scikit-learn库来实现K-Means聚类，同时讨论算法的基本原理、常用参数以及其在一个实际数据集上的应用。

数据集介绍

在本教程中，我们将使用鸢尾花数据集（Iris dataset），这是一个经典的数据集，包含三种不同种类的鸢尾花的测量特征。数据集中的每个样本有四个特征：花萼长度、花萼宽度、花瓣长度和花瓣宽度。这是一个理想的数据集，用于介绍K-Means算法，因为我们知道数据集应该包含三个簇（每个簇对应一种鸢尾花），并且每个样本都有数值型特征。

K-Means算法原理

K-Means算法是一种迭代的聚类算法，其基本原理如下：

1. 选择要分成的簇的数量K。
2. 初始化K个质心点，可以是随机选择的数据点或其他方法。
3. 将每个数据点分配给距离最近的质心。
4. 更新每个簇的质心，计算每个簇内数据点的平均值。
5. 重复步骤3和4，直到满足停止条件，例如，质心不再改变或达到最大迭代次数。

K-Means的目标是最小化每个数据点与其所属簇的质心之间的距离。这意味着相似的数据点将被分配到相同的簇中，不相似的数据点将被分配到不同的簇中。

Scikit-learn中的K-Means

Scikit-learn是一个用于机器学习和数据分析的Python库，提供了各种聚类算法的实现，包括K-Means。以下是Scikit-learn中K-Means的主要参数：

• n_clusters：要分成的簇的数量，默认为8。
• max_iter：最大迭代次数，默认为300。
• n_init：运行算法的次数，以获得最佳聚类，默认为10。
• init：初始化质心的方法，可以是"k-means++"、"random"或自定义初始化数组。
• precompute_distances：是否预先计算距离以加快计算，默认为"auto"。
• 其他参数包括tol、n_jobs、random_state等。

下面是一个使用Scikit-learn的K-Means算法的示例，使用鸢尾花数据集：

import matplotlib.pyplot as plt
import matplotlib
from sklearn.cluster import KMeans
from sklearn.datasets import load_iris

# 设置matplotlib配置
matplotlib.rcParams['font.sans-serif'] = [u'SimHei']
matplotlib.rcParams['axes.unicode_minus'] = False

# 加载鸢尾花数据集
iris = load_iris()
X = iris.data[:, :2]

# 构建K-Means模型
k = 3
km = KMeans(n_clusters=k)
km.fit(X)

# 获取样本所属簇的编号
label_pred = km.labels_
centroids = km.cluster_centers_

# 可视化未聚类和聚类后的数据分布
plt.subplot(121)
plt.scatter(X[:, 0], X[:, 1], s=50)
plt.xlabel('花萼长度')
plt.ylabel('花萼宽度')
plt.title("未聚类之前")

plt.subplot(122)
plt.scatter(X[:, 0], X[:, 1], c=label_pred, s=50, cmap='cool')
plt.scatter(centroids[:,0], centroids[:,1], c='red', marker='o', s=100)
plt.xlabel('花萼长度')
plt.ylabel('花萼宽度')
plt.title("K-Means算法聚类结果")

plt.show()

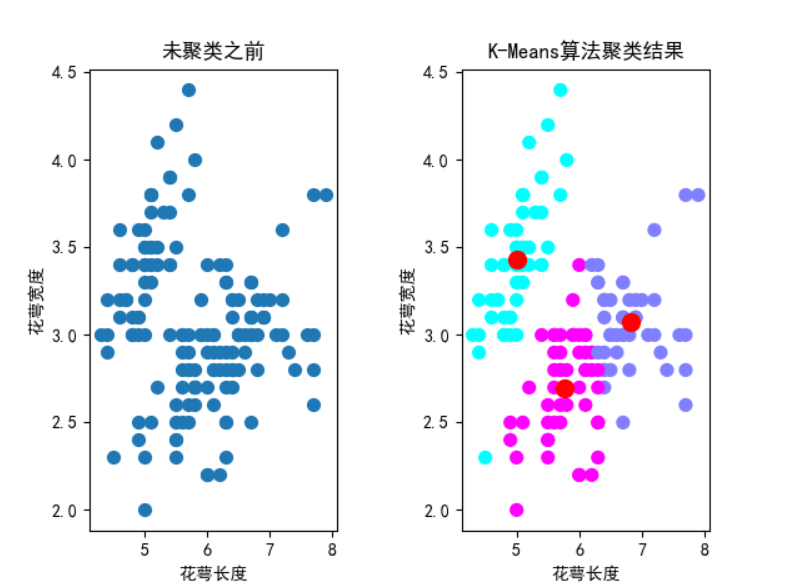
在上面的示例中，我们首先加载了鸢尾花数据集，然后创建了一个K-Means模型，将数据点分成了三个簇。最后，我们可视化了未聚类和聚类后的数据分布。

结论

K-Means算法是一种强大的聚类工具，尤其适用于数据特征是数值型的情况。Scikit-learn为您提供了一种便捷的方式来实现K-Means算法，同时提供了许多参数来调整算法的行为。通过学习和实践，您可以充分利用K-Means算法来解决各种聚类问题。

希望本文对您有所帮助，让您更好地理解K-Means算法的原理和如何在Scikit-learn中使用它。祝您在聚类分析中取得成功！

（完整示例代码和数据集可在GitHub上找到。）

参考资料

• Scikit-learn：Scikit-learn官方文档
• K-Means Clustering：维基百科上的K-Means算法介绍

---

这篇博客介绍了K-Means算法的原理、Scikit-learn中的使用以及在鸢尾花数据集上的应用示例。希望您能通过这篇博文更好地理解K-Means算法，以及如何在实