数据结构与算法分析

排序算法

排序算法是最常用的算法之一，它用于对数据集合进行排列。这里将介绍一些常见的排序算法：冒泡排序、快速排序、归并排序、插入排序、选择排序和堆排序。

1. 冒泡排序 (Bubble Sort)

冒泡排序是一种简单的排序算法，它通过重复交换相邻未按顺序排列的元素，直到整个序列按顺序排列。每一轮操作将最大元素“冒泡”到最后。

时间复杂度：

• 最坏和平均时间复杂度为 O(n²)，最好的情况下为 O(n)（当数组已经排序时）。

空间复杂度：

• O(1)，只需要常数空间。

public class BubbleSort {
    public static void bubbleSort(int[] arr) {
        int n = arr.length;
        for (int i = 0; i < n - 1; i++) {
            for (int j = 0; j < n - i - 1; j++) {
                if (arr[j] > arr[j + 1]) {
                    // 交换 arr[j] 和 arr[j + 1]
                    int temp = arr[j];
                    arr[j] = arr[j + 1];
                    arr[j + 1] = temp;
                }
            }
        }
    }
}

2. 插入排序 (Insertion Sort)

插入排序将每个元素插入到已排序的部分，逐步形成一个完整的排序序列。

时间复杂度：

• 最坏和平均时间复杂度为 O(n²)，最好的情况下为 O(n)（当数组已经排序时）。

空间复杂度：

• O(1)，只需要常数空间。

public class InsertionSort {
    public static void insertionSort(int[] arr) {
        for (int i = 1; i < arr.length; i++) {
            int key = arr[i];
            int j = i - 1;
            while (j >= 0 && arr[j] > key) {
                arr[j + 1] = arr[j];
                j = j - 1;
            }
            arr[j + 1] = key;
        }
    }
}

3. 选择排序 (Selection Sort)

选择排序每次从未排序的部分中选择最小元素，放到已排序部分的末尾。

时间复杂度：

• O(n²)，无论输入数据是否有序。

空间复杂度：

• O(1)，只需要常数空间。

public class SelectionSort {
    public static void selectionSort(int[] arr) {
        int n = arr.length;
        for (int i = 0; i < n - 1; i++) {
            int minIdx = i;
            for (int j = i + 1; j < n; j++) {
                if (arr[j] < arr[minIdx]) {
                    minIdx = j;
                }
            }
            // 交换元素
            int temp = arr[minIdx];
            arr[minIdx] = arr[i];
            arr[i] = temp;
        }
    }
}

4. 快速排序 (Quick Sort)

快速排序采用分治法，将数组分为较小的部分进行排序，最终合并。它选择一个“基准”元素，将大于基准的元素移到右边，小于基准的元素移到左边，然后递归对这两部分继续排序。

时间复杂度：

• 最坏时间复杂度为 O(n²)，最好的情况下为 O(n log n)。

空间复杂度：

• O(log n)，栈的深度。

public class QuickSort {
    public static void quickSort(int[] arr, int low, int high) {
        if (low < high) {
            int pi = partition(arr, low, high);
            quickSort(arr, low, pi - 1);
            quickSort(arr, pi + 1, high);
        }
    }

    private static int partition(int[] arr, int low, int high) {
        int pivot = arr[high];
        int i = (low - 1);
        for (int j = low; j < high; j++) {
            if (arr[j] <= pivot) {
                i++;
                int temp = arr[i];
                arr[i] = arr[j];
                arr[j] = temp;
            }
        }
        int temp = arr[i + 1];
        arr[i + 1] = arr[high];
        arr[high] = temp;
        return i + 1;
    }
}

5. 归并排序 (Merge Sort)

归并排序也是一种分治法排序算法，它将数组分成两个子数组，分别排序后合并。它具有稳定性，适合大规模数据排序。

时间复杂度：

• O(n log n)，不受输入数据的影响。

空间复杂度：

• O(n)，需要额外的空间来存储中间数组。

public class MergeSort {
    public static void mergeSort(int[] arr, int left, int right) {
        if (left < right) {
            int mid = (left + right) / 2;
            mergeSort(arr, left, mid);
            mergeSort(arr, mid + 1, right);
            merge(arr, left, mid, right);
        }
    }

    private static void merge(int[] arr, int left, int mid, int right) {
        int n1 = mid - left + 1;
        int n2 = right - mid;
        int[] L = new int[n1];
        int[] R = new int[n2];
        
        System.arraycopy(arr, left, L, 0, n1);
        System.arraycopy(arr, mid + 1, R, 0, n2);

        int i = 0, j = 0, k = left;
        while (i < n1 && j < n2) {
            if (L[i] <= R[j]) {
                arr[k++] = L[i++];
            } else {
                arr[k++] = R[j++];
            }
        }

        while (i < n1) arr[k++] = L[i++];
        while (j < n2) arr[k++] = R[j++];
    }
}

6. 堆排序 (Heap Sort)

堆排序基于完全二叉树的堆结构。它将数组视为一个二叉堆，最大堆或最小堆，然后通过反复移除根节点来构建排序序列。

时间复杂度：

• O(n log n)，无论输入数据是否有序。

空间复杂度：

• O(1)，只需要常数空间。

public class HeapSort {
    public static void heapSort(int[] arr) {
        int n = arr.length;

        // 构建最大堆
        for (int i = n / 2 - 1; i >= 0; i--) {
            heapify(arr, n, i);
        }

        // 一次次移除根节点，调整堆
        for (int i = n - 1; i >= 0; i--) {
            int temp = arr[0];
            arr[0] = arr[i];
            arr[i] = temp;

            heapify(arr, i, 0);
        }
    }

    private static void heapify(int[] arr, int n, int i) {
        int largest = i;
        int left = 2 * i + 1;
        int right = 2 * i + 2;

        if (left < n && arr[left] > arr[largest]) largest = left;
        if (right < n && arr[right] > arr[largest]) largest = right;

        if (largest != i) {
            int swap = arr[i];
            arr[i] = arr[largest];
            arr[largest] = swap;
            heapify(arr, n, largest);
        }
    }
}

---

树结构

树结构广泛应用于搜索、排序和分层数据存储等领域。常见的树包括完全二叉树、前缀树、二叉搜索树、AVL 树和红黑树。

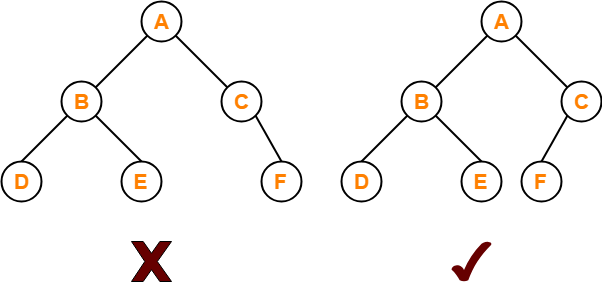
1. 完全二叉树 (Complete Binary Tree)

完全二叉树是一种特殊的二叉树，具有以下核心特点：

1. 层级填充：除了可能最后一层外，所有层都必须填满节点。
2. 靠左排列：最后一层的节点必须从左到右依次排列，不能有空隙。

换句话说，它是一棵“几乎满”的二叉树，最后一层可以不满，但节点必须集中在左侧。

基本性质

• 高度：如果树高为 $h$，前 $h-1$ 层是满的，每层有 $2^i$ 个节点（$i$ 是层号）。
• 节点数：范围在 $2^h$ 到 $2^{h+1}-1$ 之间。
• 存储方式：可以用数组表示，节点按层序排列，方便访问子节点和父节点。

2. 前缀树 (Trie)

前缀树，又称 字典树 或 Trie 树，是一种专门用于处理字符串的树形数据结构。它的核心思想是通过共享前缀来高效存储和检索一组字符串。

基本概念

1. 节点结构：

   • 每个节点代表一个字符。
   • 从根节点到某个节点的路径表示一个字符串的前缀。
   • 根节点通常是空的（不代表任何字符）。

2. 特点：

   • 共享前缀：具有相同前缀的字符串共享路径上的节点，从而节省存储空间。
   • 叶子节点或标记：通常用一个特殊标记（比如布尔值 isEnd）表示从根到该节点是否构成一个完整的单词。

3. 用途：

   • 快速查找某个字符串是否存在。
   • 检索具有特定前缀的所有字符串（前缀查询）。
   • 常用于自动补全、拼写检查、字典实现等。

简单例子

假设要存储字符串 "cat"、"car" 和 "dog"：

       (根)
      / | \
     c  d  ...
    /   |
   a    o
  / \   |
 t   r  g

• 路径 c -> a -> t 表示 "cat"。
• 路径 c -> a -> r 表示 "car"。
• 路径 d -> o -> g 表示 "dog"。
• "ca" 是 "cat" 和 "car" 的共享前缀。

3. 二叉搜索树 (BST)

**二叉搜索树（Binary Search Tree, BST）**是一种特殊的二叉树，每个节点的值大于左子树所有值，小于右子树所有值。它支持高效的搜索、插入、删除，时间复杂度取决于树高 $O(h)$。中序遍历会得到递增序列，但如果不平衡（比如递增插入 1, 2, 3），会退化成链表，效率变低。可以用平衡树（如 AVL 或红黑树）改进。

简单例子

假设有一棵 BST：

       5
      / \
     3   7
    / \   \
   1   4   8

• 根节点是 5。
• 左子树 (3, 1, 4) 都小于 5。
• 右子树 (7, 8) 都大于 5。
• 中序遍历结果：1, 3, 4, 5, 7, 8（递增顺序）。

基本操作

1. 搜索：
   • 从根开始，若目标值小于当前节点值，去左子树；若大于，去右子树；相等则找到。
   • 时间复杂度：$O(h)$，$h$ 是树高。
2. 插入：
   • 类似搜索，找到合适位置插入新节点。
   • 时间复杂度：$O(h)$。
3. 删除：
   • 删除节点时需调整树结构（分情况：无子节点、一个子节点、两个子节点）。
   • 时间复杂度：$O(h)$。

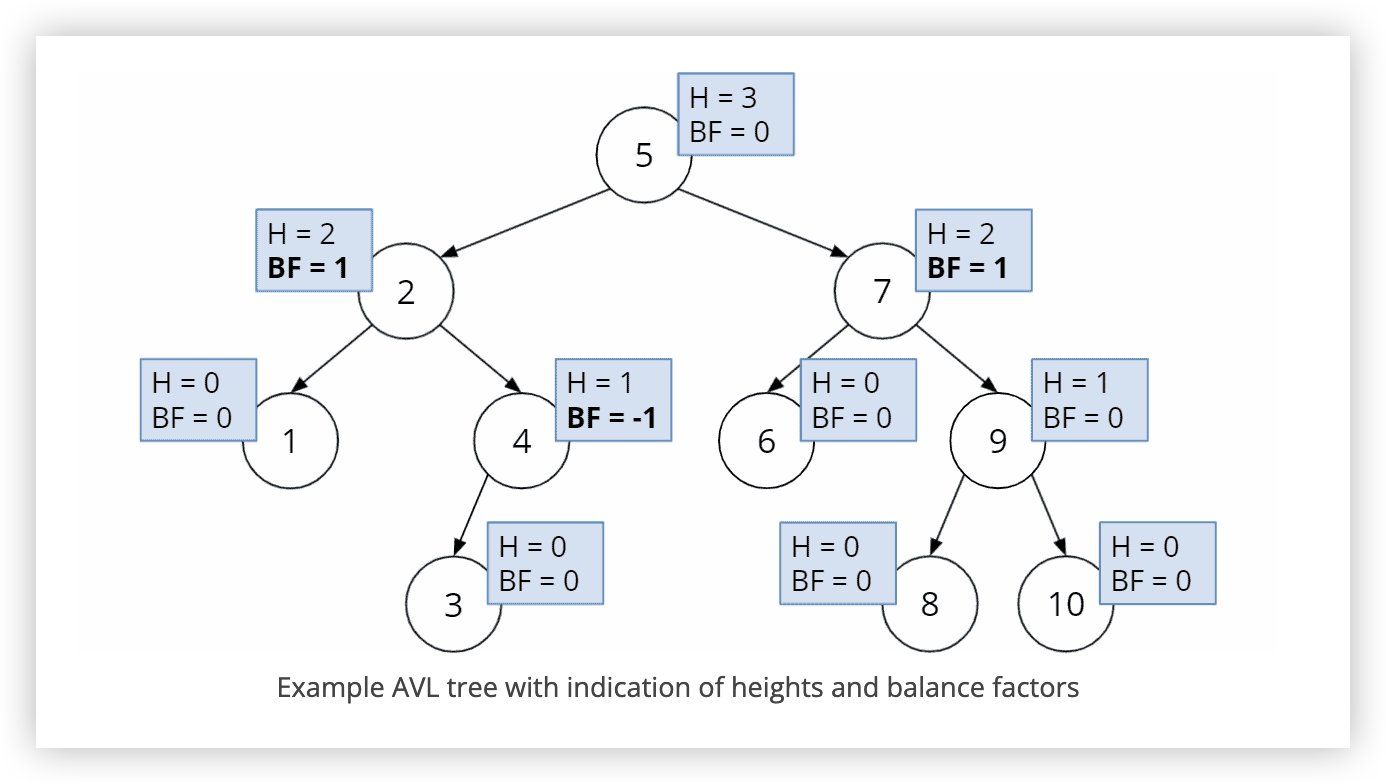
4. AVL 树

AVL 树是一种自平衡的二叉搜索树，确保任意节点的左右子树高度差（平衡因子）不超过 1，从而在最坏情况下也能保持 O(log n) 的时间复杂度。

时间复杂度：

• 查找操作： 由于树的高度被限制在 O(log n)，查找操作的时间复杂度为 O(log n)。
• 插入和删除操作：在最坏情况下，插入和删除操作需要进行旋转调整，以维持树的平衡，时间复杂度仍为 O(log n)。

空间复杂度：

• AVL 树的空间复杂度为 O(n)，其中 n 是树中节点的数量。

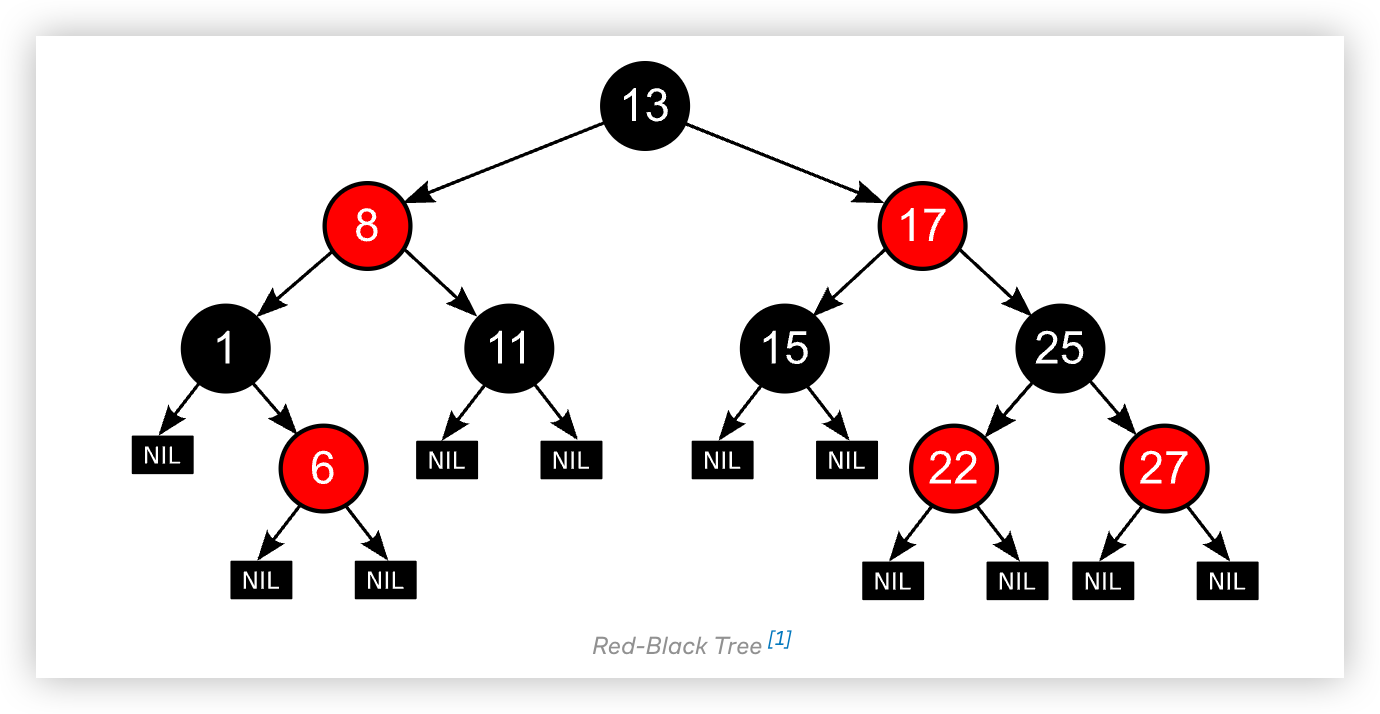
5. 红黑树

红黑树是一种自平衡的二叉搜索树，每个节点带有红色或黑色属性，通过五条规则保持平衡：根节点为黑色、叶子（NIL）为黑色、红色节点的子节点必须为黑色、从根到叶子的每条路径黑色节点数相同、节点非红即黑。这些规则确保树高最多为 $O(\log n)$，提供高效操作。插入或删除时，通过颜色调整和旋转维持平衡，相比 AVL 树调整更灵活。

时间复杂度：

• 查找操作： 由于树高被限制在 $O(\log n)$，查找操作的时间复杂度为 $O(\log n)$。
• 插入和删除操作： 在最坏情况下，插入和删除需要颜色调整和旋转以维持平衡，时间复杂度仍为 $O(\log n)$。

空间复杂度：

• 红黑树的空间复杂度为 $O(n)$，其中 $n$ 是树中节点的数量。

6. B 树与 B+ 树

B树和B+树是两种高效的多路平衡搜索树，广泛应用于数据库和文件系统中，用于管理大量数据并优化磁盘访问。以下是它们的核心特点和对比：

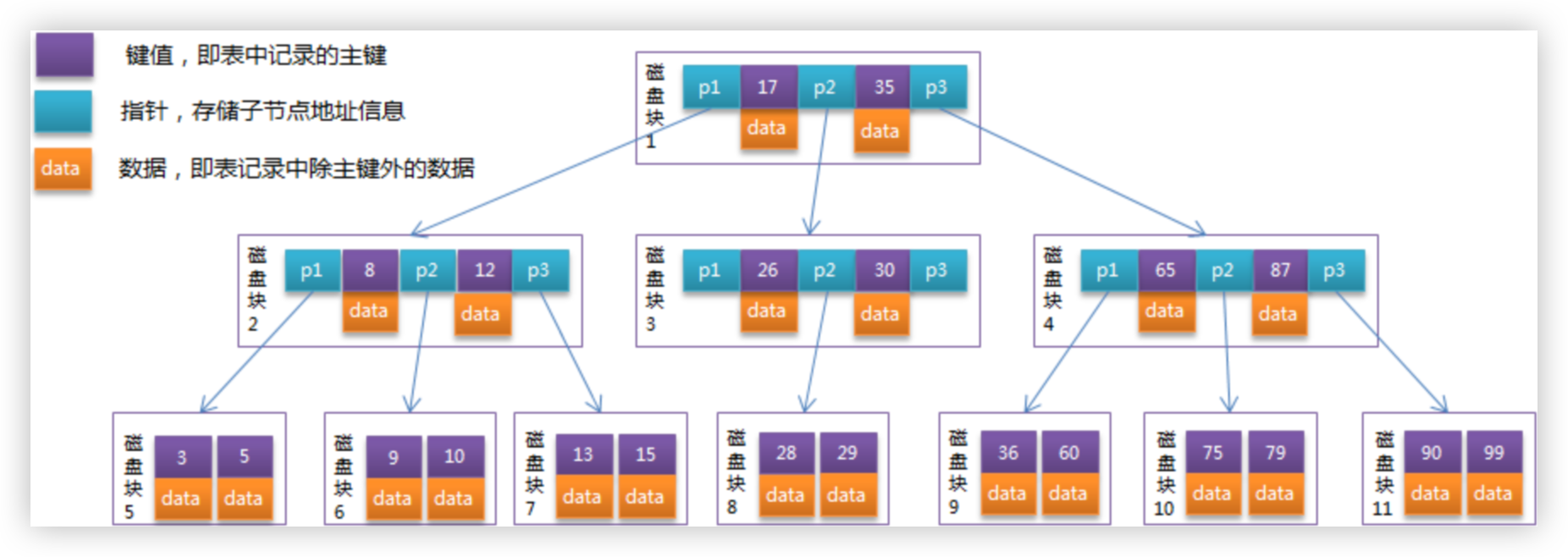
1. B树（B-Tree）

特点：

• 多路平衡：每个节点最多有 m 个子节点（m 阶B树），且所有叶子节点在同一层。
• 键值分布：每个节点包含多个键（k 个）和子节点指针（k+1 个），键按升序排列，子节点键值范围由其父节点键分割。
• 数据存储：所有节点都可能存储数据（键关联实际数据或指针）。

优势：

• 减少磁盘I/O：矮胖的树形结构降低树的高度，减少磁盘访问次数。
• 平衡性：插入、删除时通过分裂、合并节点自动维持平衡。
• 适用场景：适合读写操作混合且数据量大的场景，如文件系统（NTFS、ReiserFS）。

示例：

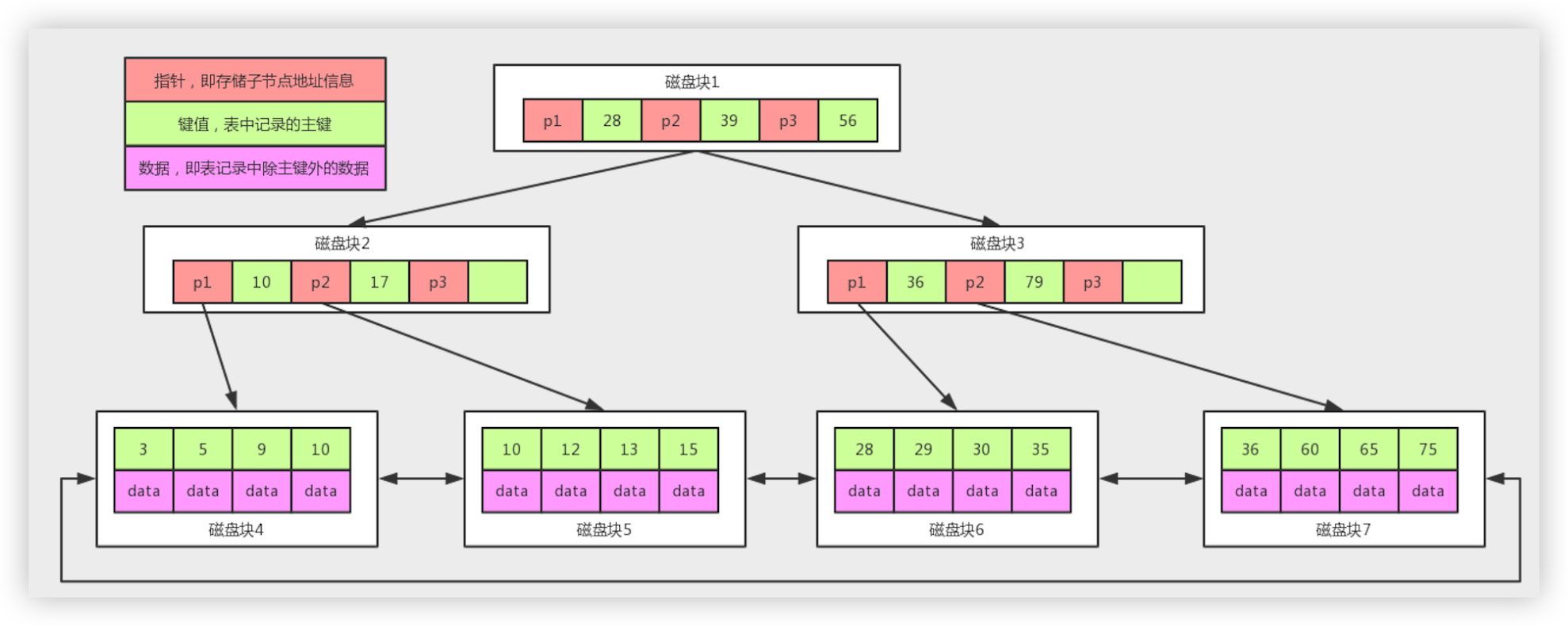
2. B+树（B+ Tree）

特点：

• 数据仅存于叶子：内部节点仅存储键和子节点指针，所有数据记录集中在叶子节点。
• 叶子链表：叶子节点通过指针形成有序链表，支持高效的范围查询。
• 键冗余：内部节点的键会在叶子节点中重复出现（作为子树的最大/最小值）。

优势：

• 更稳定的查询：任何查询都需到叶子节点，时间复杂度一致。
• 高效范围查询：链表结构直接遍历叶子节点即可，无需回溯树。
• 更优的磁盘I/O：内部节点可存储更多键，进一步降低树的高度。
• 适用场景：数据库索引（如MySQL InnoDB），强调范围查询和顺序访问。

示例：

3. 对比

特性	B树	B+树
数据存储位置	所有节点均可存数据	仅叶子节点存储数据
叶子节点结构	独立，无链表连接	通过指针形成有序链表
查询稳定性	可能在内部节点命中，时间不固定	必须到叶子节点，时间稳定
范围查询效率	低效（需中序遍历）	高效（直接遍历叶子链表）
空间利用率	内部节点存储数据，占用更多空间	内部节点仅存键，空间利用率更高
适用场景	文件系统、特定数据库（MongoDB）	关系型数据库（MySQL）、大数据索引

跳表

跳表（Skip List）是一种随机化的数据结构，本质上是对有序链表的优化 —— 通过在链表基础上增加 “索引层”，实现快速查询、插入和删除操作，平均时间复杂度可达 O (log n)，性能接近平衡树（如红黑树），但实现更简单。

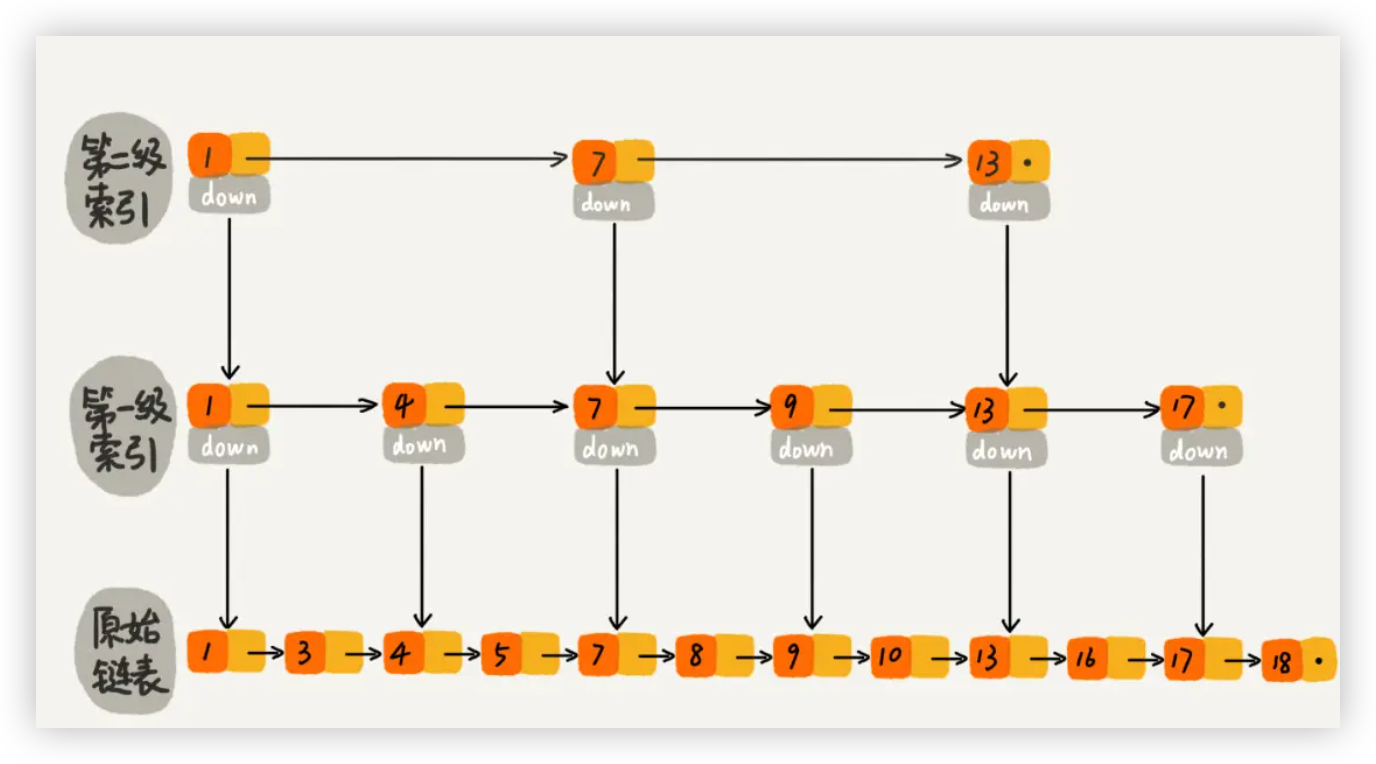
1. 跳表的核心结构

跳表的底层是一个有序链表（节点按 key 从小到大排列），在此基础上增加了多层 “索引”：

• 最底层（Level 0）是完整的有序链表，包含所有节点；
• 上层索引（Level 1, 2, ..., k）是对下层链表的 “抽样”，每个索引节点指向下层对应节点，用于快速跳过部分节点；
• 索引层级越高，节点越稀疏（类似金字塔结构）。

示例：
假设底层链表为 1 → 3 → 5 → 7 → 9，可能的索引结构：

• Level 1（上层索引）：1 → 5 → 9（每个节点间隔 1 个底层节点）；
• Level 2（更高层索引）：1 → 9（间隔 3 个底层节点）；
  查询时，从最高层索引开始，快速跳过不可能包含目标的区间，最终定位到底层节点。

2. 跳表的核心操作

1. 查询

• 从最高层索引的头节点开始，沿当前层向右遍历：
  • 若下一个节点的 key ≤ 目标 key，继续向右；
  • 若下一个节点的 key > 目标 key，下降到下一层，重复上述过程；
  • 直到在底层链表找到目标节点（或确认不存在）。

优势：通过高层索引跳过大量节点，避免遍历整个链表（时间复杂度从 O (n) 优化为 O (log n)）。

2. 插入

• 先通过查询逻辑找到插入位置；
• 随机生成索引层级：新节点插入底层后，通过随机算法（如抛硬币）决定是否晋升到上层索引（层级越高，概率越低，通常最高层级有上限）；
• 逐层插入索引节点，指向下层对应节点。

随机层级的意义：避免索引层级集中，保证跳表的 “平衡性”（类似平衡树的旋转作用，但实现更简单）。

3. 删除

• 先找到目标节点及其所有层级的索引节点；
• 从最高层开始，逐层删除索引节点，最后删除底层链表节点。

面试题

1.为什么 HashMap 选用红黑树而不选择 AVL 树？

在 JDK 1.8 中，HashMap 当链表长度超过阈值（默认 8）时会转为红黑树，主要原因是红黑树在插入、删除操作的效率上优于 AVL 树，更适合 HashMap 的动态场景。

• AVL 树：是一种严格平衡的二叉搜索树，要求左右子树高度差不超过 1，因此插入 / 删除时可能需要频繁旋转（最多 O (log n) 次），虽然查询效率极高（O (log n)），但维护成本高。
• 红黑树：是一种 “近似平衡” 的二叉搜索树，通过颜色规则（红黑节点交替、根黑叶黑等）保证最长路径不超过最短路径的 2 倍，插入 / 删除时旋转次数更少（最多 2 次），虽然查询效率略低于 AVL 树，但整体动态性能更优。

HashMap 的场景特点是插入和删除频繁，且对查询效率的要求无需 “严格平衡”（近似平衡已足够），因此红黑树的性价比更高。

2.为什么数据库索引选择 B + 树而不选择其他树（如 B 树、二叉搜索树）？

数据库索引需要适配磁盘 IO 特性（读写速度慢、按页读取），B + 树的结构设计恰好能最小化磁盘 IO 次数，同时优化范围查询。

1. 与二叉搜索树（如红黑树）对比：

   • 二叉搜索树的高度较高（O (log n)，但基数大时绝对高度大），会导致磁盘 IO 次数多（每一层对应一次 IO）。
   • B + 树是多路平衡查找树，一个节点可以存储多个关键字（如 1000 个），因此高度极低（通常 3-4 层），能大幅减少 IO 次数（3-4 次 IO 即可完成查询）。

2. 与 B 树对比：

   • B 树的非叶子节点也存储数据，导致每个节点存储的关键字数量少，高度更高，且范围查询需要回溯（非叶子节点数据分散）。

   • B + 树的

     所有数据都存储在叶子节点

     ，且叶子节点通过链表串联，非叶子节点仅作为索引。这一设计有两个优势：

     • 范围查询效率极高（直接遍历叶子节点链表）；
     • 非叶子节点仅存索引，单个节点可容纳更多关键字，进一步降低树高，减少 IO。

因此，B + 树在磁盘 IO 效率和范围查询上的优势，使其成为数据库索引的最优选择。

3.为什么 Redis 的 Zset（有序集合）选择跳表而不选择其他数据结构（如红黑树、B + 树）？

Zset 需要支持插入、删除、查询、范围排名等操作，跳表（Skip List）的实现简单且性能稳定，适合 Redis 的内存数据库场景。

• 跳表：是一种随机化的数据结构，通过在链表上增加 “索引层” 实现快速查询，平均时间复杂度为 O (log n)，插入 / 删除时只需修改相邻索引，实现简单（无需旋转等复杂操作）。
• 红黑树：虽然也能实现 Zset 的功能（如按分数排序），但范围查询（如ZRANGE）需要中序遍历，实现复杂度高，且 Redis 追求代码简洁（跳表逻辑更简单，易于维护）。
• B + 树：多路结构适合磁盘场景，但在内存中无需考虑 IO 效率，且跳表的单值查询、插入效率与 B + 树相当，实现更简单。

Redis 的场景特点是内存操作（无需考虑磁盘 IO），且需要兼顾实现复杂度和性能，跳表的 “随机化平衡” 机制既保证了 O (log n) 的平均性能，又避免了红黑树的复杂旋转逻辑，因此被选为 Zset 的底层实现（Redis 中 Zset 实际是跳表与哈希表的结合，哈希表用于快速查询元素分数）。