在本教程中，我们将使用k最近邻（k-Nearest Neighbors，kNN）算法对数据进行分类。k最近邻算法是一种简单而有效的监督学习算法，用于根据最近邻样本的标签将新样本分类到不同的类别中。

步骤1：准备数据

首先，我们需要准备数据集。我们将使用一个名为Social_Network_Ads.csv的数据集，其中包含了用户的一些特征数据和他们是否购买了某个商品。你可以在Social_Network_Ads.csv下载数据集。

步骤2：导入必要的库和模块

我们将使用Python编写代码并使用VuePress进行展示。以下是所需的库和模块：

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier
from sklearn.metrics import confusion_matrix

步骤3：读取数据

让我们读取数据集并将特征数据和目标变量分别存储在X和Y中：

dataset = pd.read_csv('path/to/Social_Network_Ads.csv')
X = dataset.iloc[:, [2, 3]].values
Y = dataset.iloc[:, 4].values

步骤4：数据划分

为了评估算法的性能，我们将数据集划分为训练集和测试集。我们将使用train_test_split函数将数据集划分为75%的训练集和25%的测试集：

X_train, X_test, y_train, y_test = train_test_split(X, Y, test_size=0.25, random_state=0)

步骤5：特征缩放

由于k最近邻算法基于距离度量，我们需要对特征进行缩放，以确保它们具有相同的尺度。我们将使用StandardScaler进行特征缩放：

sc = StandardScaler()
X_train = sc.fit_transform(X_train)
X_test = sc.transform(X_test)

步骤6：训练模型和预测

现在我们可以使用k最近邻算法对训练集数据进行训练，并对测试集进行预测：

classifier = KNeighborsClassifier(n_neighbors=5, metric='minkowski', p=2)
classifier.fit(X_train, y_train)
y_pred = classifier.predict(X_test)

在这里，KNeighborsClassifier是sklearn库中实现k最近邻算法的分类器类。它的参数说明如下：

• n_neighbors：指定用于分类的最近邻数目。
• metric：指定距离度量方法，常用的有'minkowski'、'euclidean'和'manhattan'等。
• p：当metric='minkowski'时，指定闵可夫斯基距离的幂参数。

步骤7：评估模型

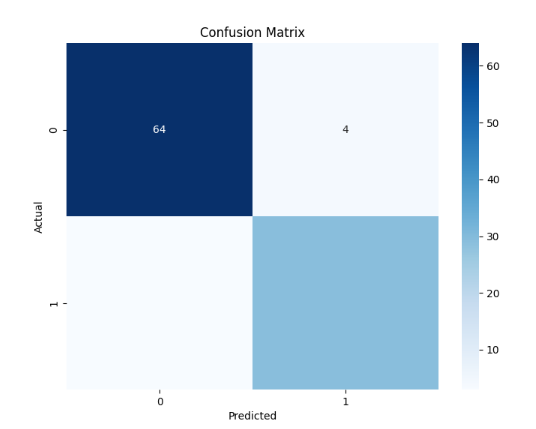
混淆矩阵（Confusion Matrix）是一种评估分类器性能的常用工具，特别用于对分类模型的预测结果进行可视化和统计分析。它以表格的形式展示了分类模型在不同类别上的预测结果与真实标签之间的对应关系。

混淆矩阵的表格结构如下所示：

              预测为正例    预测为反例
真实为正例    True Positive (TP)    False Negative (FN)
真实为反例    False Positive (FP)   True Negative (TN)

• True Positive (TP) 表示模型正确地将正例样本预测为正例。
• False Negative (FN) 表示模型错误地将正例样本预测为反例。
• False Positive (FP) 表示模型错误地将反例样本预测为正例。
• True Negative (TN) 表示模型正确地将反例样本预测为反例。

混淆矩阵可以帮助我们计算和理解以下评估指标：

1. 准确率（Accuracy）：分类器正确预测的样本数占总样本数的比例，计算公式为 (TP + TN) / (TP + TN + FP + FN)。
2. 精确率（Precision）：在分类器预测为正例的样本中，实际为正例的比例，计算公式为 TP / (TP + FP)。
3. 召回率（Recall）：在实际为正例的样本中，分类器预测为正例的比例，计算公式为 TP / (TP + FN)。
4. F1值（F1 Score）：综合考虑精确率和召回率的指标，计算公式为 2 * (Precision * Recall) / (Precision + Recall)。

通过混淆矩阵的分析，我们可以获得分类器在不同类别上的预测性能情况，进而对其进行评估和比较。例如，我们可以判断分类器是否存在偏差或错误地将某一类别样本预测为另一类别的情况。

总之，混淆矩阵是一种有助于评估分类器性能的工具，它提供了对分类模型预测结果的更详细和全面的认识，特别是在多类别分类问题中。

我们可以使用混淆矩阵来评估分类器的性能：

cm = confusion_matrix(y_test, y_pred)
# 创建热力图
plt.figure(figsize=(8, 6))
sns.heatmap(cm, annot=True, fmt='d', cmap='Blues')

# 设置坐标轴标签和标题
plt.xlabel('Predicted')
plt.ylabel('Actual')
plt.title('Confusion Matrix')

# 显示图形
plt.show()

confusion_matrix是sklearn库中用于计算混淆矩阵的函数。

步骤8：可视化结果

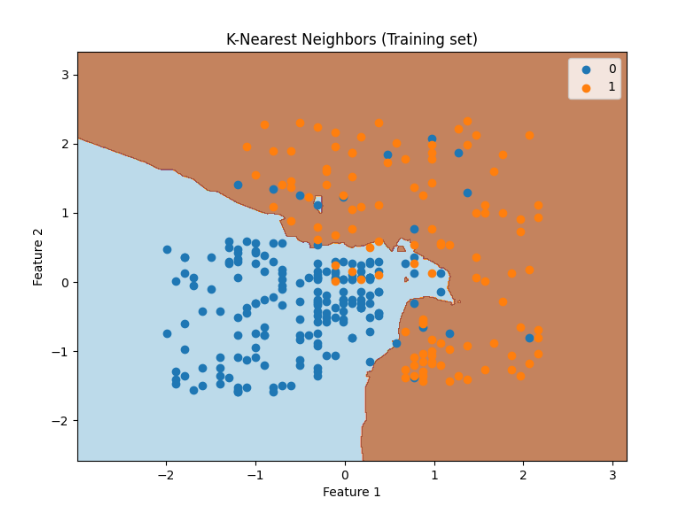
最后，我们可以使用matplotlib库将训练集和测试集的结果可视化。使用contourf函数绘制了分类边界，并使用散点图展示了训练集的特征点，其中类别0用蓝色表示，类别1用橙色表示。添加了标题、横轴和纵轴标签，并显示图形。

plt.figure(figsize=(8, 6))
X_set, y_set = X_train, y_train
X1, X2 = np.meshgrid(
    np.arange(start=X_set[:, 0].min() - 1, stop=X_set[:, 0].max() + 1, step=0.01),
    np.arange(start=X_set[:, 1].min() - 1, stop=X_set[:, 1].max() + 1, step=0.01)
)
plt.contourf(X1, X2, classifier.predict(np.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape), alpha=0.75, cmap='Paired')
plt.xlim(X1.min(), X1.max())
plt.ylim(X2.min(), X2.max())
for i, j in enumerate(np.unique(y_set)):
    plt.scatter(X_set[y_set == j, 0], X_set[y_set == j, 1], c='tab:blue' if j == 0 else 'tab:orange', label=j)
plt.title('K-Nearest Neighbors (Training set)')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.legend()
plt.show()

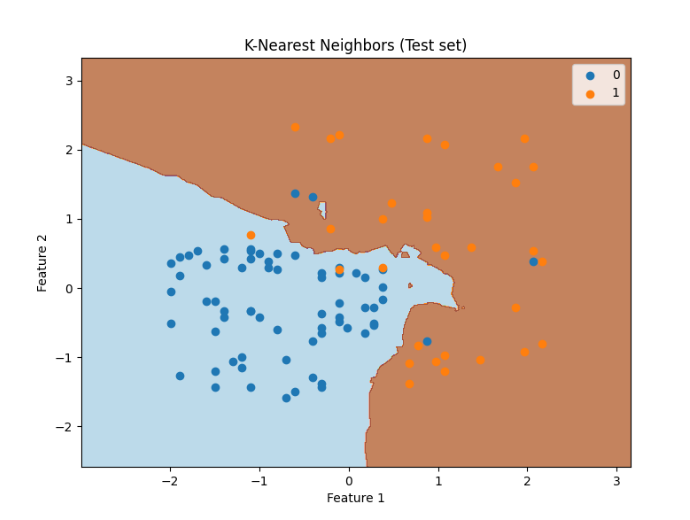
# Visualize the test set results
plt.figure(figsize=(8, 6))
X_set, y_set = X_test, y_test
X1, X2 = np.meshgrid(
    np.arange(start=X_set[:, 0].min() - 1, stop=X_set[:, 0].max() + 1, step=0.01),
    np.arange(start=X_set[:, 1].min() - 1, stop=X_set[:, 1].max() + 1, step=0.01)
)
plt.contourf(X1, X2, classifier.predict(np.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape), alpha=0.75, cmap='Paired')
plt.xlim(X1.min(), X1.max())
plt.ylim(X2.min(), X2.max())
for i, j in enumerate(np.unique(y_set)):
    plt.scatter(X_set[y_set == j, 0], X_set[y_set == j, 1], c='tab:blue' if j == 0 else 'tab:orange', label=j)
plt.title('K-Nearest Neighbors (Test set)')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.legend()
plt.show()